Пример.

Классификация методов криптографического преобразования информации

Лекция 11. Криптографические методы защиты информации

Вопросы:

11.1. Классификация методов криптографического преобразования информации

11.2. Стандарты шифрования

11.3. Перспективы использования криптозащиты информации в КС

 

Литература:

1. Завгородний В.И. комплексная защита информации в компьютерных системах: Учебное пособие. – Логос, 201. – С.159-179.

 

Под криптографической защитой информации понимается такое преобразование исходной информации, в результате которого она становится недоступной для ознакомления и использования лицами, не имеющими на это полномочий.

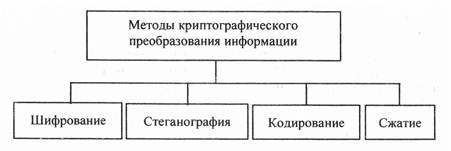
Известны различные подходы к классификации методов криптографического преобразования информации. По виду воздействия на исходную информацию методы криптографического преобразования информации могут быть разделены на четыре группы (рис.11.1).

Процесс шифрования заключается в проведении обратимых математических, логических, комбинаторных и других преобразований исходной информации, в результате которых зашифрованная информация представляет собой хаотический набор букв, цифр, других символов и двоичных кодов.

Рис.11.1. Классификация методов криптографического преобразования информации

 

Для шифрования информации используются алгоритм преобразования и ключ. Как правило, алгоритм для определенного метода шифрования является неизменным. Исходными данными для алгоритма шифрования служат информация, подлежащая зашифрованию, и ключ шифрования. Ключ содержит управляющую информацию, которая определяет выбор преобразования на определенных шагах алгоритма и величины операндов, используемые при реализации алгоритма шифрования.

В отличие от других методов криптографического преобразования информации, методы стеганографии [2] позволяют скрыть не только смысл хранящейся или передаваемой информации, но и сам факт хранения или передачи закрытой информации. В компьютерных системах практическое использование стеганографии только начинается, но проведенные исследования показывают ее перспективность. В основе всех методов стеганографии лежит маскирование закрытой информации среди открытых файлов. Обработка мультимедийных файлов в КС открыла практически неограниченные возможности перед стеганографией.

Существует несколько методов скрытой передачи информации. Одним из них является простой метод скрытия файлов при работе в операционной системе MS DOS. За текстовым открытым файлом записывается скрытый двоичный файл, объем которого много меньше текстового файла. В конце текстового файла помещается метка EOF (комбинация клавиш Control и Z). При обращении к этому текстовому файлу стандартными средствами ОС считывание прекращается по достижению метки EOF и скрытый файл остается недоступен. Для двоичных файлов никаких меток в конце файла не предусмотрено. Конец такого файла определяется при обработке атрибутов, в которых хранится длина файла в байтах. Доступ к скрытому файлу может быть получен, если файл открыть как двоичный. Скрытый файл может быть зашифрован. Если кто-то случайно обнаружит скрытый файл, то зашифрованная информация будет воспринята как сбой в работе системы.

Графическая и звуковая информация представляются в числовом виде. Так в графических объектах наименьший элемент изображения может кодироваться одним байтом. В младшие разряды определенных байтов изображения в соответствии с алгоритмом криптографического преобразования помещаются биты скрытого файла. Если правильно подобрать алгоритм преобразования и изображение, на фоне которого помещается скрытый файл, то человеческому глазу практически невозможно отличить полученное изображение от исходного. Очень сложно выявить скрытую информацию и с помощью специальных программ. Наилучшим образом для внедрения скрытой информации подходят изображения местности: фотоснимки со спутников, самолетов и т.п. С помощью средств стеганографии могут маскироваться текст, изображение, речь, цифровая подпись, зашифрованное сообщение. Комплексное использование стеганографии и шифрования многократно повышает сложность решения задачи обнаружения и раскрытия конфиденциальной информации.

Содержанием процессакодирования информации является замена смысловых конструкций исходной информации (слов, предложений) кодами. В качестве кодов могут использоваться сочетания букв, цифр, букв и цифр. При кодировании и обратном преобразовании используются специальные таблицы или словари. Кодирование информации целесообразно применять в системах с ограниченным набором смысловых конструкций. Такой вид криптографического преобразования применим, например, в командных линиях АСУ. Недостатками кодирования конфиденциальной информации является необходимость хранения и распространения кодировочных таблиц, которые необходимо часто менять, чтобы избежать раскрытия кодов статистическими методами обработки перехваченных сообщений.

Сжатие информации может быть отнесено к методам криптографического преобразования информации с определенными оговорками. Целью сжатия является сокращение объема информации. В то же время сжатая информация не может быть прочитана или использована без обратного преобразования. Учитывая доступность средств сжатия и обратного преобразования, эти методы нельзя рассматривать как надежные средства криптографического преобразования информации. Даже если держать в секрете алгоритмы, то они могут быть сравнительно легко раскрыты статистическими методами обработки. Поэтому сжатые файлы конфиденциальной информации подвергаются последующему шифрованию. Для сокращения времени целесообразно совмещать процесс сжатия и шифрования информации.

11.1.1. Шифрование. Основные понятия

Основным видом криптографического преобразования информации в КС является шифрование. Подшифрованием понимается процесс преобразования открытой информации в зашифрованную информацию(шифртекст) или процесс обратного преобразования зашифрованной информации в открытую. Процесс преобразования открытой информации в закрытую получил названиезашифрование, а процесс преобразования закрытой информации в открытую -расшифрование.

За многовековую историю использования шифрования информации человечеством изобретено множество методов шифрования или шифров. Методом шифрования (шифром) называется совокупность обратимых преобразований открытой информации в закрытую информацию в соответствии с алгоритмом шифрования. Большинство методов шифрования не выдержали проверку временем, а некоторые используются и до сих пор. Появление ЭВМ и КС инициировало процесс разработки новых шифров, учитывающих возможности использования ЭВМ как для зашифрования/расшифрования информации, так и для атак на шифр. Атака на шифр(криптоанализ) - это процесс расшифрования закрытой информации без знания ключа и, возможно, при отсутствии сведений об алгоритме шифрования.

Современные методы шифрования должны отвечать следующим требованиям:

- стойкость шифра противостоять криптоанализу(криптостойкость) должна быть такой, чтобы вскрытие его могло быть осуществлено только путем решения задачи полного перебора ключей;

- криптостойкость обеспечивается не секретностью алгоритма шифрования, а секретностью ключа;

- шифртекст не должен существенно превосходить по объему исходную информацию;

- ошибки, возникающие при шифровании, не должны приводить к искажениям и потерям информации;

- время шифрования не должно быть большим;

- стоимость шифрования должна быть согласована со стоимостью закрываемой информации.

Криптостойкость шифра является его основным показателем эффективности. Она измеряется временем или стоимостью средств, необходимых криптоаналитику для получения исходной информации по шифртексту, при условии, что ему неизвестен ключ.

Сохранить в секрете широко используемый алгоритм шифрования практически невозможно. Поэтому алгоритм не должен иметь скрытых слабых мест, которыми могли бы воспользоваться криптоаналитики. Если это условие выполняется, то Криптостой­кость шифра определяется длиной ключа, так как единственный путь вскрытия зашифрованной информации - перебор комбинаций ключа и выполнение алгоритма расшифрования. Таким образом, время и средства, затрачиваемые на криптоанализ, зависят от длины ключа и сложности алгоритма шифрования.

В качестве примера удачного метода шифрования можно привести шифр DES (Data Encryption Standard), применяемый в США с 1978 года в качестве государственного стандарта. Алгоритм шифрования не является секретным и был опубликован в открытой печати. За все время использования этого шифра не было обнародовано ни одного случая обнаружения слабых мест в алгоритме шифрования.

В конце 70-х годов использование ключа длиной в 56 бит гарантировало, что для раскрытия шифра потребуется несколько лет непрерывной работы самых мощных по тем временам компьютеров. Прогресс в области вычислительной техники позволил значительно сократить время определения ключа путем полного перебора. Согласно заявлению специалистов Агентства национальной безопасности США 56-битный ключ для DES может быть найден менее чем за 453 дня с использованием суперЭВМ Cray T3D, которая имеет 1024 узла и стоит 30 млн. долл. Используя чип FPGA (Field Progammably Gate Array - программируемая вентильная матрица) стоимостью 400 долл., можно восстановить 40-битный ключ DES за 5 часов. Потратив 10000 долл. за 25 чипов FPGA, 40-битный ключ можно найти в среднем за 12 мин. Для вскрытия 56-битного ключа DES при опоре на серийную технологию и затратах в 300000 долл. требуется в среднем 19 дней, а если разработать специальный чип, то - 3 часа. При затратах в 300 млн. долл. 56-битные ключи могут быть найдены за 12 сек. Расчеты показывают, что в настоящее время для надежного закрытия информации длина ключа должна быть не менее 90 бит.

Все методы шифрования могут быть классифицированы по различным признакам. Один из вариантов классификации приведен на рис.11.2 [8].

Рис.11.2. Классификация методов шифрования

11.1.3. Методы шифрования с симметричным ключом

1. Методы замены

Сущность методов замены (подстановки) заключается в замене символов исходной информации, записанных в одном алфавите, символами из другого алфавита по определенному правилу |56]. Самым простым является метод прямой замены. Символам s_0i, исходного алфавита A₀, с помощью которых записывается исходная информация, однозначно ставятся в соответствие символы s_1i, шифрующего алфавита A₁. В простейшем случае оба алфавита могут состоять из одного и того же набора символов. Например, оба алфавита могут содержать буквы русского алфавита.

Задание соответствия между символами обоих алфавитов осуществляется с помощью преобразования числовых эквивалентов символов исходного текста. Т₀, длиной - К символов, по определенному алгоритму.

Алгоритм моно алфавитной замены может быть представлен в виде последовательности шагов.

Шаг 1. Формирование числового кортежа L_0h путем замены каждого символа s_0i Î T₀ (i = l,K), представленного в исходном алфавите А₀ размера [1´R], на число h_0i(s_0i), соответствующее порядковому номеру символа s_0i в алфавите А₀.

Шаг 2. Формирование числового кортежа L_1h путем замены каждого числа кортежа L_0h на соответствующее число h_1i кортежа L_1h, вычисляемое по формуле:

h_1i = (k₁´h_0i(s_0i)+k₂)(mod R),

где k₁ - десятичный коэффициент;

k₂ - коэффициент сдвига.

Выбранные коэффициенты k₁, k₂ должны обеспечивать однозначное соответствие чисел h_0i и h_1i;, а при получении h_1i = 0 выполнить замену h_1i=R.

Шаг 3. Получение шифртекста T₁ путем замены каждого числа h_1i(s_1i,) кортежа L_1h соответствующим символом s_1i Î T₁ (i = l,K) алфавита шифрования а₁ размера [1´R].

Шаг 4. Полученный шифртекст разбивается на блоки фиксированной длины b. Если последний блок оказывается неполным, то в конец блока помещаются специальные символы-заполнители (например, символ *).

Пример. Исходными данными для шифрования являются:

Т₀=<МЕТОД_ШИФРОВАНИЯ>;

А₀=<АБВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩ ЪЫЬЭЮЯ_>;

А₁=<ОРЩЬЯТЭ_ЖМЧХАВДЫФКСЕЗПИЦГНЛЪШБУЮ>;

К=32; k₁=3; k₂=15, b=4.

Пошаговое выполнение алгоритма приводит к получению следующих результатов.

Шаг 1. L_0h=<12,6,18,14,5,32,24,9,20,16,14,3,U3,9,31>.

Шаг 2. L_1h=<19,l,5,25,30,15,23,10,ll,31,25,24,18,22,10,12>.

Шаг З.Т₁=<СОЯГБДИМЧУГЦКПМХ>.

Шаг 4.Т₂=<СОЯГ БДИМ ЧУГЦ КПМХ>.

При расшифровании сначала устраняется разбиение на блоки. Получается непрерывный шифртекст T₁ длиной К символов. Расшифрование осуществляется путем решения целочисленного уравнения:

k₁ h_0i + k₂ = n R + h_1i,

При известных целых величинах k1, k2, h1i и R величина h0ш вычисляется методом перебора n.

Последовательное применение этой процедуры ко всем символам шифртекста приводит к его расшифрованию.

По условиям приведенного примера может быть построена таблица замены, в которой взаимозаменяемые символы располагаются в одном столбце (табл.1).

 

Использование таблицы замены значительно упрощает процесс шифрования. При шифровании символ исходного текста сравнивается с символами строки s_0i таблицы. Если произошло совпадение в i-м столбце, то символ исходного текста заменяется символом из строки s_1i;, находящегося в том же столбце i таблицы.

Расшифрование осуществляется аналогичным образом, но вход в таблицу производится по строке s_1i.

Основным недостатком метода прямой замены является наличие одних и тех же статистических характеристик исходного и закрытого текста. Зная, на каком языке написан исходный текст и частотную характеристику употребления символов алфавита этого языка, криптоаналитик путем статистической обработки перехваченных сообщений может установить соответствие между символами обоих алфавитов.

Существенно более стойкими являются методы полиалфавитной замены. Такие методы основаны на использовании нескольких алфавитов для замены символов исходного текста. Формально полиалфавитную замену можно представить следующим образом. При N - алфавитной замене символ s_0i из исходного алфавита A₁ заменяется символом s₁₁ из алфавита A₁, s₀₂ заменяется символом s₂₂ из алфавита А₂ и так далее. После замены s_0N символом s_NN из i A_N символ s_0(N+1) замещается символом s_1(N+1) из алфавита A₁ и так далее (рис.11.3).

Рис.11.3. Матрица Вижинера

Шифрование осуществляется с помощью ключа, состоящего из М неповторяющихся символов. Из полной матрицы Вижинера выделяется матрица шифрования Т_Ш, размерностью [(M+1),R]. Она включает первую строку и строки, первые элементы которых совпадают с символами ключа. Если в качестве ключа выбрано <ЗОНД>, то матрица шифрования содержит пять строк (рис.11.4).

 

Рис.11.4. Матрица шифрования для ключа <ЗОНД>

Алгоритм зашифрования с помощью таблицы Вижинера представляет собой следующую последовательность шагов.

Шаг 1. Выбор ключа К длиной М символов.

Шаг 2. Построение матрицы шифрования Т_Ш=(b_ij) размерностью [(M+1),R] для выбранного ключа К.

Шаг 3. Под каждым символом s_0r исходного текста длиной I символов размещается символ ключа k_m (рис.20). Ключ повторяется необходимое число раз.

Шаг 4. Символы исходного текста последовательно замещаются символами, выбираемыми из Т_Ш по следующему правилу:

1) определяется символ k_m ключа К, соответствующий заменяемому символу s_0r;

2) находится строка i в Т_Ш,для которой выполняется условие k_m=b_i1;

3) определяется столбец j, для которого выполняется условие: s_0r = b_1j;

4) символ s_0r замещается символом b_ij,

Шаг 5. Полученная зашифрованная последовательность разбивается на блоки определенной длины, например, по четыре символа. Последний блок дополняется, при необходимости, случайными символами до полного объема.

Расшифрование осуществляется в следующей последовательности:

Шаг 1. Под шифртекстом записывается последовательность символов ключа по аналогии с шагом 3 алгоритма зашифрования.

Шаг 2. Последовательно выбираются символы s_1r из шифртекста и соответствующие символы ключа k_m. В матрице Т_Ш определяется строка i, для которой выполняется условие k_m= b_i1. В строке i определяется элемент b_ij= s_1r. В расшифрованный текст на позицию r помещается символ b_1j.

Шаг 3. Расшифрованный текст записывается без разделения на блоки. Убираются служебные символы.

Требуется с помощью ключа К = <ЗОНД> зашифровать исходный текст Т = <БЕЗОБЛАЧНОЕ_НЕБО>. Механизмы зашифрования и расшифрования представлены на рис.11.5.

 

Рис.11.5. Пример шифрования с помощью матрицы Вижинера

 

Криптостойкость методов полиалфавитной замены значительно выше методов простой замены, так как одни и те же символы исходной последовательности могут заменяться разными символами. Однако стойкость шифра к статистическим методам криптоанализа зависит от длины ключа.

Для повышения криптостойкости может использоваться модифицированная матрица шифрования. Она представляет собой матрицу размерности [11,R], где R - число символов алфавита. В первой строке располагаются символы в алфавитном порядке. Остальные 10 строк нумеруются от 0 до 9. В этих строках символы располагаются случайным образом.

В качестве ключей используются, например, непериодический бесконечные числа p, e и другие. Очередной n-й символ исходного текста заменяется соответствующим символом из строки матрицы шифрования, номер которой совпадает с n-й цифрой бесконечного числа.