Квантование энергии

Способ получения энергии в реакторе на медленных нейтронах – лишь первая попытка. Вспомним, что делящийся материал (уран-235) составляет лишь 0,7% в достаточно дорогой урановой руде. А что делать с 99,3% урана – 238? Сам по себе этот материал не способен к делению. Но способен к делению плутоний – 239, полученный в результате бета – распада этого изотопа урана.

По мере «выгорания» в реакторе урана-235, плутоний начинает вносить все больший вклад в энергетический выход. Этот материал не исчерпывается до конца. Отработанные тепловые элементы обогащены плутонием, который можно сравнительно легко выделить химическим путем и переработать в новый делящийся материал высокой эффективности.

В результате появляется возможность полностью использовать весь природный уран, превращая его в плутоний. Этот процесс называется размножением ядерного горючего, а сами реакторы такого типа – реакторами – размножителями, или бридерами.

Более эффективен реактор, работающий не на медленных, а на быстрых нейтронах. Чтобы «запустить» такой реактор, нужно в качестве горючего использовать урановую руду, обогащенную ураном-235 не менее чем до 15%. В таком исходном сырье реакция деления урана-235 начинается без использования замедлителя.

Реактор на быстрых нейтронах является установкой для осуществления цепной реакции деления ядер изотопа урана – 235, и одновременно установкой для получения из широко распространенного и относительно дешевого изотопа урана-238 нового ядерного горючего, плутония – 239.

В реакторах на быстрых нейтронах возможно использовать для получения энергии не только редкий изотоп урана – 235, но и изотоп урана-238, которого в природе в 140 раз больше

Условная классификация ядерных реакций
по роду участвующих в реакциях частиц	реакции под действием нейтронов; реакции под действием заряженных частиц (например, протонов, α-частиц).
по роду участвующих в реакциях ядер	реакции на легких ядрах (А < 50); реакции на средних ядрах; реакции на тяжелых ядрах (А > 150)
по энергии вызывающих их частиц	реакции на малых, средних и высоких энергиях.
по характеру происходящих ядерных превращений	реакции с испусканием нейтронов; реакции с испусканием заряженных частиц.
Реакция деления ядра	Тяжелое ядро под действием нейтронов, а как впоследствии оказалось, и других частиц делится на несколько более легких ядер (осколков), чаще всего на два ядра, близких по массе.
Нейтроны деления	В случае тяжелых ядер 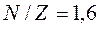. Образовавшиеся осколки деления перегружены нейтронами, в результате чего они и выделяют нейтроны деления.
Пример реакции деления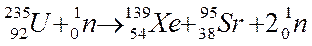
Цепная реакция деления	Ядерная реакция, в которой частицы, вызывающие реакцию, образуются как продукты реакции.
Необходимое условие для развития цепной реакции	Коэффициент размножения нейтронов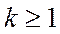
Коэффициент размножения нейтронов	Отношение числа нейтронов в данном поколении к их числу в предыдущем поколении.
Самоподдерживающаяся реакция	Реакция, при которой число нейтронов с течением времени не изменяется (при k = 1).
Развивающаяся реакция	Реакция, при которой число делений непрерывно растет, и реакция может стать взрывной (при k > 1).
Затухающая реакция	Реакция при k < 1
Термоядерная реакция	Реакция синтеза легких атомных ядер в более тяжелые, происходящая при сверхвысокой температуре (10⁷ К и выше).
Реакция синтеза атомных ядер	Образование из легких ядер более тяжелых.
Пример реакции синтеза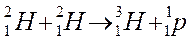
Биологическое действие радиоактивных излучений
Доза излучения	Характеристика воздействия излучений на живые организмы.
Поглощенной дозы излучения	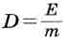Е – поглощенная энергия ионизирующего излучения m – масса облучаемого вещества
Единица поглощенной дозы излучения	Название – грей (1 Гр = 1 Дж/кг)
Естественный фон радиации (космические лучи, радиоактивность окружающей среды и человеческого тела) составляет за год дозу излучения около 2•10^–3 Гр на человека.
Для лиц, работающих с излучением, предельно допустимую за год дозу 0,05 Гр.
Доза излучения 3—10 Гр, полученная за короткое время, смертельна.
Рентген	На практике широко используется внесистемная единица экспозиционной дозы излучения — рентген (сокращенно: Р). Эта единица является мерой ионизирующей способности рентгеновского и гамма-излучений.
Доза излучения равна одному рентгену (1 Р), если в 1 см³ сухого воздуха при температуре 0°С и давлении 760 мм рт. ст. образуется столько ионов, что их суммарный заряд каждого знака в отдельности равен 3·10^–10 Кл. При этом получается примерно 2·10⁹ пар ионов.
Число образующихся ионов связано с поглощаемой веществом энергией.
В практической дозиметрии можно считать 1 Р приблизительно эквивалентным поглощенной дозе излучения 0,01 Гр.

1.1 Частица в бесконечно глубокой потенциальной яме

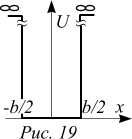У физиков есть очень популярная модель, с помощью которой часто удается понять многие свойства разнообразных физических систем по крайней мере на качественном уровне. Эта модель представляет собой частицу, заключенную между двумя абсолютно непроницаемыми для нее стенками. Условия, в которых находится частица, задаются потенциальной ямой с бесконечно высокими стенками. Пусть ширина ямы равна b, а масса частицы m. Потенциальная энергия частицы внутри ямы равна нулю, а вне ямы - бесконечности, т.е. вне ямы частицу застать нельзя. Работа, которую надо совершить, чтобы вынуть ее из ямы, равна бесконечности. Это обеспечивает непроницаемость стенки. Наша задача состоит в том, чтобы дать квантовое описание состояния частицы.

Задача описания состояния решена, если удалось найти распределение амплитуды вероятностей в этом состоянии. Найдем распределение. Поскольку частица внутри ямы свободна, распределение амплитуд пребывания частицы в точках внутри ямы должно представлять собой описанную ранее волновую конфигурацию стрелок, вращающихся с угловой скоростью w=E/ћ(E - энергия частицы). Данное распределение обладает одним недостатком - модули всех амплитуд вероятности застать частицу в любой точке ямы одинаковы. Но ведь заранее известно, что амплитуды должны равняться нулю снаружи ямы. Получается, что при переходе через границу ямы амплитуда вероятности должна скачком измениться от конечного значения до нуля. Такое распределение разрывно. Квантовая теория говорит, что распределение амплитуд обладает упругостью и не может изменяться скачком. Поэтому следует искать такое распределение, при котором ход изменения амплитуды вероятности плавно переходит от нуля за пределами к ненулевым значениям внутри ямы.

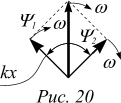Указанным требованиям удовлетворяет суперпозиция волн одинакового размаха, бегущих навстречу друг другу. В этом случае распределение амплитуд представляет собой стоячую волну. Пусть k - волновое число волны амплитуды вероятности, бегущей слева направо, тогда волновое число волны, бегущей справа налево, равно -k. Стрелки обеих волн вращаются в одну и ту же сторону. Разность фаз вращения стрелок в точке x равна 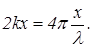Таким образом, если модули волн амплитуд вероятности равны (y1=y2=y0), то, по теореме косинусов, результирующая амплитуда вероятности равна

(4)

Распределение амплитуд должно удовлетворять требованию: в точках x=±b/2 амплитуда должна обращаться в ноль.Формула (4) допускает такую возможность, но не при любом значении k. Волновое число должно принимать только значения -

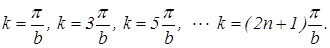(5)

Заметим, требованию равенства нулю амплитуды вероятности на границах ямы может удовлетворять не только функция (4), но и

y(x)= 2y₀∙sinkx (6)

при следующих значениях волнового числа:

(7)

Итак, можно сделать вывод, что распределение амплитуд вероятности частицы в бесконечно глубокой потенциальной яме описывается либо законом синуса, либо законом косинуса. Объединим ограничения (5) и (7), налагаемые на волновое число:

(8)

Из условия (8) вытекает важное следствие: модуль импульса частицы p=ћk также может принимать только дискретный ряд значений:

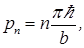(9)

где n принимает только целые значения: 1, 2, 3,...Полная энергия частицы Eравна кинетической энергии, поэтому

(10)

Это энергетический спектр частицы. Выражение (10) показывает, что 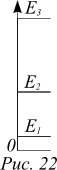энергия частицы в потенциальной яме квантуется. Квантованный энергетический спектр называют дискретным.

Зависимость от времени амплитуды вероятности частицы находиться в состоянии с определенным значением энергии сводится к вращению стрелок, изображающих амплитуды. Так что, глядя на рисунок 21 с примером распределения амплитуд, надо иметь в виду, что все стрелки и весь график распределения амплитуд вращаются. При этом модули амплитуд не изменяются во времени. Из этого следует, что вероятность застать частицу в состоянии с определенной энергией не изменяется со временем.

Или, можно провести такие рассуждения. Так как амплитуда вероятности частицы, находящейся в состоянии с определенной энергией, зависит от времени по закону , вероятность застать частицу в этом состоянии равная

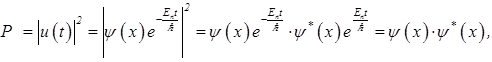(4)

не зависит от времени. По этой причине состояние с определенной энергией называют стационарным состоянием.

Вопрос 1. Пусть частица в яме находится в состоянии с определенным значением энергии. В этом случае, в соответствии с (10), можно считать, что p2также имеет определенное значение - неопределенность значения импульса равна нулю. Но при этом неопределенность координаты не превышает b.Кажется, что возникает противоречие принципу неопределенности. В чем ошибка рассуждений?

Задача 5. Частица массы mнаходится в бесконечно глубокой прямоугольной потенциальной яме ширины b в стационарном состоянии на энергетическом уровне №n. Найдите силу, с которой частица при этом давит на стенки ямы.

Решение. При изменении параметра b энергия каждого уровня изменяется. Сила направлена в сторону убывания энергии и равна минус производной от энергии по координате стенки ямы:

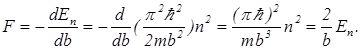(11)

Сила давления растет при сжатии ямы и с ростом номера уровня.

1.2 Обобщение

Строгая квантовая теория показывает, что частицы, находящиеся в ограниченной области пространства, всегда имеют дискретный энергетический спектр. Строгий расчет дает, что энергетический спектр электрона в атоме водорода точно такой же, какой дает теория Бора.

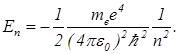(12)

Атомные спектры также являются дискретными, так как электроны в атомах движутся в ограниченной области пространства.

Другой пример - спектр энергий гармонического осциллятора -

(13)

где w - собственная частота колебаний осциллятора, n=0, 1, 2, ...

Гармонический осциллятор - чрезвычайно распространенная в природе физическая система. Системы одинаковых связанных осцилляторов интересны тем, что в них распространяются волны. Ранее было показано, что несколько упруго связанных между собой осцилляторов ведут себя как ряд невзаимодействующих гармонических осцилляторов - мод, каждая из которых движется, как одномерный гармонический осциллятор со своей частотой. Например, натянутая с силой Fструна, длины L и линейной плотностью r имеет целый ряд собственных частот, которые задаются формулой -

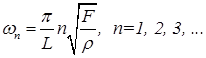(14)

Струна может колебаться с одной из этих частот (в одной моде). При этом струна имеет конфигурацию стоячей волны (моды струны - стоячие волны). Согласно квантовой механике, энергетический спектр струны представляет собой наложение спектров вида (13) всех мод.

Стоячие электромагнитные волны - тоже гармонические осцилляторы. Переходы стоячих волн на высшие уровни рассматриваются как рождение новых фотонов.

1.3 Примеры задач

Задача 6.Волна амплитуды вероятности частицы в трехмерном потенциальном ящике размером Lx´Ly´Lzимеет волновой вектор с компонентами kx, ky, kz. Задача об описании состояний частицы в таком ящике распадается на три независимые одномерные задачи, решенные на настоящем занятии.
а) Найдите разрешенные значения проекций волнового вектора частицы.
б) Как выглядит энергетический спектр частицы?
в) В ящике находится N частиц. Полагая, что в состоянии теплового равновесия средние значения квадратов проекций волновых чисел равны между собой, определите давление частиц на стенки ящика. Выразите давление через среднее значение энергии одной частицы.