Свойства энтропии
3.1 Аддитивность энтропии
Полная энтропия термодинамической системы равна сумме энтропий частей. Это мы наблюдали в рассмотренных выше примерах.
3.2 Энтропия является функцией состояния
В определении энтропии фигурирует теплота, которая зависит от способа передачи, т.е. не являющаяся функцией состояния. А изменение энтропии 
, тем не менее, является функцией состояния. Это означает, что если термодинамическая система участвует в циклическом процессе, то ее энтропия не изменяется.
Задача. Рассмотрим три способа попадания одного моля идеального газа из состояния с объемом V0 при давлении 4P0 в состояние с объемом 4V0 при давлении P0. В первом способе газ изохорически охлаждается, пока давление не уменьшится до P0. Потом газ изобарически расширился до объема 4V0. Во втором способе газ вначале изобарически расширился до объема 4V0, а потом изохорически остывает до давления P0. В третьем способе газ расширялся изотермически. Вычислить изменения энтропии в каждом из трех процессов.
Решение. В процессе A–C температура изменяется. Надо считать поэлементно. Имеем 
. Изменение энтропии в элементарном процессе равно
. (2.12)
Полное изменение энтропии в процессе A–C равно
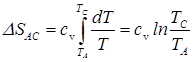(2.13)
Из уравнения состояния идеального газа имеем 
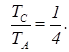Поэтому 
.
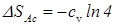В процессе C–B температура так же изменяется. Имеем 
. Изменение энтропии в элементарном процессе равно
. (2.14)
Полное изменение энтропии в процессе C–B равно
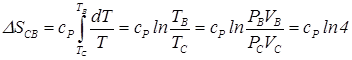(2.15)
Итого изменение энтропии в процессе A–C–B равно
(2.15)
Аналогичную последовательность расчетов проводим для процесса A–D–B.
(2.16)
(2.16)
(2.17)
Получилось точно столько же.
В изотермическом процессе температура не изменяется. Полное изменение энтропии равно отношению поглощенного тепла к температуре изотермы
(2.18)
Из уравнения Майера 
. Получилось точно то же самое, что и для первых двух процессов. Можно было бы придумать какой-нибудь другой путь от A к B, и получилось бы то же самое. Данный пример подтверждает утверждение, что изменение энтропии является функцией состояния, как и изменение внутренней энергии.