Силы, действующие между частицами твердого тела

Классификация кристаллов по типам сил связи

Лекция 4

4.1 Силы, действующие между частицами твердого тела

4.2 Ионные кристаллы

4.3 Атомные кристаллы

4.4 Металлические кристаллы

4.5 Молекулярные кристаллы

4.6 Кристаллы с водородными связями

4.7 Сопоставление различных типов связей

Классификация кристаллов по кристаллическим системам дает представление о геометрических характеристиках кристалла, но не затрагивает вопроса о природе сил, удерживающих атомы (молекулы или ионы) в определенных местах – в узлах кристаллической решетки.

Можно произвести классификацию кристаллов по другому принципу, а именно: в зависимости от физической природы сил, действующих между частицами кристалла. Тогда мы получим четыре типа кристаллов (кристаллических решеток): ионные, атомные, металлические и молекулярные.

Классификация кристаллов, основанная на типах сил связи, позволяет сделать некоторые обобщения относительно свойств и поведения кристаллов, чего нельзя сделать, рассматривая только геометрию решеток.

До сих пор мы не учитывали природу сил, удерживающих частицы в строго упорядоченном положении. На самом деле необходимо учитывать природу этих сил, так как она определяет энергию связи в решетке и основные ее свойства. Рассмотрим силы взаимодействия и соответственно энергию связи для двухчастичной модели (рисунок 4.1).

Пусть мы имеем две частицы, одна из которых расположена в начале координат, а вторая – в бесконечности и из бесконечности приближается к первой частице.

Сила притяжения обычно описывается следующей формулой:

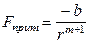где b и m – постоянные целые числа и зависят от природы решетки.

По мере сближения частиц при малых r резко возрастает сила отталкивания.

Обычно полагают

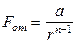где a и n – целые постоянные числа, зависящие от типа решетки.

Для того чтобы силы отталкивания при малых расстояниях между частицами превышали силу притяжения, необходимо, чтобы n > m (для некоторых кристаллов полагают n = 12, m = 6).

Тогда суммарную силу взаимодействия можно представить в виде:

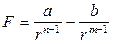Зная, что

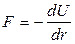можно показать, что суммарная потенциальная энергия взаимодействия системы 2-х частиц U определяется формулой:

где , .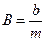