Трансформатор

Рис. 13.1. Электрическая цепь с взаимной индукцией

Схема замещения индуктивно связанных элементов

Вариометр

Автотрансформатор

Трансформатор

Схема замещения индуктивно связанных элементов

Трансформаторы

ЛЕКЦИЯ 13

 

План лекции:

 

Рассмотрим случай двух индуктивно связанных катушек, представляющих собой трансформатор без ферромагнитного сердечника (рис. 13.1).

 

 

Составим уравнения электрической цепи, учитывая, что токи катушек направлены встречно по отношению к одноимённым выводам:

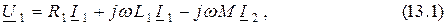
Преобразуем эти уравнения.

Полученным уравнениям соответствует схема с электрической (рис. 13.2), а не с индуктивной связью между катушками. Эта схема является эквивалентной схемой замещения индуктивно связанных катушек. Она позволяет рассчитывать цепи любым из известных методов, например, методами узловых напряжений или контурных токов, чего нельзя сделать для схемы с индуктивной связью. Вертикальную ветвь называют ветвью намагничивания.

 

Рис. 13.2. Т-образная схема замещения индуктивно связанных катушек без ферромагнитного сердечника

 

Если катушки индуктивности одинаковые, то есть , то, как следует из уравнения (12.10), выполняются неравенства и . Такая схема может быть реализована практически.

Если катушки индуктивности разные, то одна из индуктивностей в горизонтальных ветвях схемы замещения 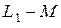или может оказаться отрицательной. В этом случае при практической реализации эквивалентной схемы отрицательную индуктивность можно заменить эквивалентной ёмкостью. При изменении частоты сопротивление индуктивности изменяется пропорционально, а сопротивление ёмкости – обратно пропорционально изменению частоты. Поэтому эквивалентная схема с отрицательной индуктивностью практически может быть реализована только на одной частоте.

Данная схема замещения является не единственной.

Обозначим через полное сопротивление первого контура, то есть сумму сопротивлений, по которым протекает ток . Отсюда

.

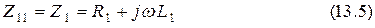Обозначим аналогично через полное сопротивление второго контура. Поэтому

Сопротивление, принадлежащее обоим контурам, назовём сопротивлением связи и обозначим как . Весьма часто имеет место соотношение и поэтому можно считать . В данном случае (рис. 13.2) имеем

.

Выразим ток второго контура через ток первого , используя уравнение (13.2),

и подставим результат в уравнение (13.1)

Заменяя в формуле (13.8) ток первого контура через выражение (13.9), получаем

Уравнениям (13.9) и (13.10) соответствует схема с раздельными контурами (рис. 13.3), являющаяся эквивалентной схемой замещения цепи с трансформаторной связью (рис. 13.1). Здесь

– вносимое сопротивление в первый контур со стороны второго,

 

Рис. 13.3. Двухконтурная развязанная схема замещения индуктивно связанных катушек

 

– вносимое сопротивление во второй контур со стороны первого,

– вносимая эдс во второй контур со стороны первого.

Так как полное сопротивление второго контура (13.6) зависит от сопротивления нагрузки, то вносимое сопротивление в первый контур (13.11) также зависит от .

 

Трансформатором называют устройство, передающее энергию из одной цепи в другую с помощью электромагнитной индукции. Трансформатор состоит из двух или большего числа индуктивно связанных обмоток – катушек индуктивности. Катушки трансформатора для увеличения степени связи конструктивно располагают соосно или на общем замкнутом сердечнике. Коэффициент связи (12.7) между обмотками в трансформаторе считают максимальным и равным 1, то есть

Обмотку трансформатора, в которую поступает энергия от внешнего источника, называют первичной, все остальные обмотки – вторичными.

Если сердечник отсутствует или выполнен из неферромагнитного материала, то трансформатор можно рассматривать как линейную электрическую цепь.

Ферромагнитный сердечник применяют для увеличения магнитного потока и связи между обмотками трансформатора. Это позволяет повысить величину передаваемой мощности во вторичную обмотку. Трансформатор с ферромагнитным сердечником является нелинейным устройством. Однако его конструируют так, чтобы он по своим свойствам приближался к идеальному трансформатору и имел малую нелинейность. Поэтому трансформатор с ферромагнитным сердечником практически всегда также рассматривают как линейную электрическую цепь.

Коэффициентом трансформации называют отношение напряжения на вторичной обмотке к первичной:

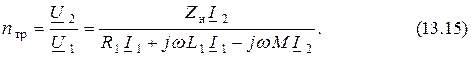
Весьма часто разработчиков интересует отношение токов в трансформаторе, называемое коэффициентом трансформации по току. Получим его из формулы (13.8):

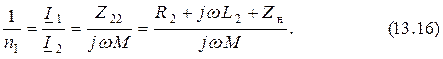
Оба коэффициента трансформации зависят от вида и величины сопротивления нагрузки.

В реальных трансформаторах активные сопротивления собственных потерь и весьма малы по сравнению с реактивными и поэтому можно принять . Такой трансформатор называют совершенным. Для него уравнения (13.1) и (13.2) преобразуются к виду

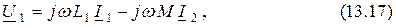
Выражая ток из уравнения (13.18) и подставляя его в (13.17), получаем

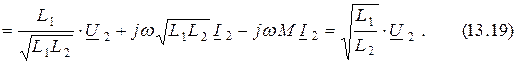
С учётом того, что индуктивность катушки пропорциональна квадрату числа витков, находим коэффициент трансформации по напряжению

Следовательно, коэффициент трансформации совершенного трансформатора равен отношению числа витков вторичной обмотки к первичной и не зависит от сопротивления нагрузки. Различают повышающие и понижающие трансформаторы.

Преобразуя выражение (13.16), получаем

Отношение токов в отличие от напряжений зависит от сопротивления нагрузки. Кроме того, у повышающего трансформатора ток вторичной обмотки меньше, чем ток в первичной обмотке, а у понижающего – наоборот.