Согласное и встречное включение индуктивностей
Выводы двух индуктивно связанных катушек, относительно которых токи направлены одинаково и направления создаваемых ими потоков самоиндукции и взаимной индукции в каждой катушке совпадают, называют одноимёнными, а включение катушек – согласным. Иначе говоря, одноимённые зажимы двух катушек обладают той особенностью, что подведение к одной из них возрастающего тока приводит к повышению потенциала на одноимённом зажиме другой катушки.
Если же потоки будут направлены встречно, то выводы катушек, относительно которых направления токов совпадают, называют разноимёнными, а включение катушек – встречным. На принципиальных электрических схемах одноимённые выводы обозначают каким-либо одинаковым знаком, например, "звёздочкой" (*), точкой или другим.
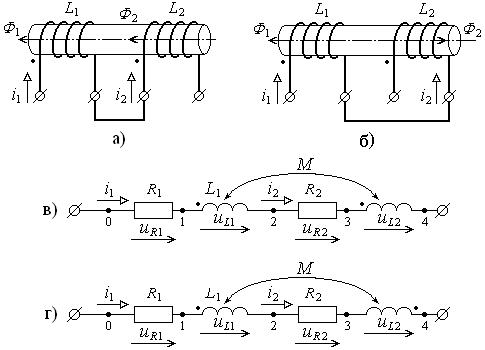
Рис. 12.2. Согласное (а, в) и встречное (б, г) включение катушек индуктивности
В связи с введением понятия одноимённых выводов при вычерчивании электрических схем нет необходимости показывать намотку витков катушек индуктивности, а достаточно разметить на схеме их одноимённые зажимы и выбранные положительные направления токов (рис. 12.2).
12.3. Комплексная форма расчёта цепей с взаимными индуктивностями
Соединим две индуктивно связанные катушки последовательно так, чтобы полный магнитный поток каждой из катушек увеличился, то есть включим катушки согласно (рис. 12.2, в).
На основании закона Фарадея эдс самоиндукции первой катушки в комплексной форме записи равна

Электродвижущая сила взаимоиндукции при согласном включении катушек будет иметь такой же знак, как и  , то есть
, то есть

Подобные соотношения имеют место и для второй индуктивности.
Учитывая, что  , составим уравнение для нахождения напряжения в случае согласованного включения катушек:
, составим уравнение для нахождения напряжения в случае согласованного включения катушек:
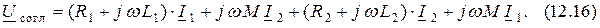
Так как 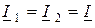 , то получим
, то получим
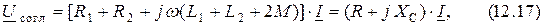
где 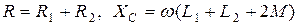 .
.
При последовательном встречном включении катушек индуктивности (рис. 12.2, г) уравнение напряжения на выводах схемы будет равно:
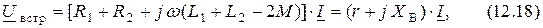
где  .
.
На рис. 12.3 приведены топографические векторные диаграммы для согласного и встречного последовательного соединения двух катушек индуктивности.
Два последних уравнения указывают способ нахождения величины взаимоиндукции  . Для этого надо измерить реактивные составляющие полных сопротивлений при согласном и встречном включении индуктивностей и вычесть их
. Для этого надо измерить реактивные составляющие полных сопротивлений при согласном и встречном включении индуктивностей и вычесть их
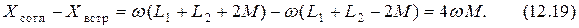

Рис. 12.3. Векторные диаграммы последовательно включенных согласно (а) и встречно (б) индуктивно связанных катушек
Отсюда получаем выражение

которое позволяет по экспериментальным данным рассчитать величину взаимной индукции.