Основные понятия об индуктивно связанных цепях

Согласное и встречное включение индуктивностей

Основные понятия об индуктивно связанных цепях

ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ

ИНДУКТИВНО СВЯЗАННЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

 

План лекции:

12.3. Комплексная форма расчёта цепей с взаимными индуктивностями

 

Индуктивно связанными называют электрические цепи, содержащие, по крайней мере, две индуктивности, магнитные потоки которых проходят не только через их собственные витки, но и через витки другой индуктивности.

Предположим, что даны две катушки индуктивности , расположенные в достаточной близости друг от друга так, что магнитное поле каждой из них пересекает витки другой (рис. 12.1). Катушки не обязательно должны быть соосными, как это показано на рисунке. Они могут быть расположены параллельно или под любым углом друг к другу.

При протекании тока силовые линии магнитного потока катушки замыкаются, проходя как внутри катушки, так и через окружающее её пространство, при этом часть магнитных силовых линий одной катушки пересекает, а часть не пересекает витки другой катушки.

Часть магнитного потока, которая замыкается в пространстве и не пересекает витки другой катушки, называют потоком рассеяния и обозначают символом .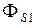

 

Рис. 12.1. Индуктивно связанные катушки индуктивности

 

Другую часть магнитного потока первой катушки, которая пересекает витки второй катушки и создаёт в ней магнитное поле, называют потоком взаимной индукции . Первый индекс обозначает номер катушки, в которой создаётся поле, второй – номер катушки, создающей поле. Поэтому полный поток самоиндукции первой катушки может быть записан в виде

Полный магнитный поток катушки индуктивности является алгебраической суммой потоков всех её витков. Этот магнитный поток часто называют потокосцеплением самоиндукции и обозначают через .

Взаимной индукцией называют наведение эдс в электрической цепи при изменении магнитного поля в другой цепи.

Взаимной индуктивностью первой катушки со второй 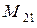называют от­ношение потокосцепления взаимной индукции к связанному с ним току, то есть к току, который создаёт этот магнитный поток (потокосцепление)

Аналогично ток второй катушки создаёт магнитный поток самоиндукции 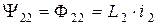, часть которого пересекает витки первой катушки, а часть рассеивается, так что

Таким образом, полный магнитный поток катушки индуктивности состоит из потока самоиндукции и потока взаимоиндукции. Магнитные силовые линии имеют направления. Поэтому под потоком понимают сумму проекций силовых магнитных линий на перпендикулярное направление к площади поперечного сечения витка. Следовательно, потоки самоиндукции и взаимоиндукции могут либо совпадать по направлению, либо быть направлены встречно. Поэтому полный магнитный поток – полное потокосцепление – может быть как меньше, так и больше потока самоиндукции

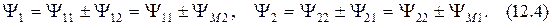
С учётом вышеизложенного получаем, что

и

Для линейных электрических цепей всегда выполняется равенство

и поэтому индекс у взаимной индуктивности может быть опущен.

Величина взаимной индуктивности зависит от взаимного расположения катушек индуктивности.

Например, с увеличением расстояния между катушками увеличиваются их потоки рассеивания и уменьшаются потоки взаимоиндукции (потокосцепление между катушками). Поэтому взаимная индуктивность уменьшается.

Отклонение от соосности или параллельности приводит к уменьшению суммы проекций силовых магнитных линий потока взаимной индукции на перпендикулярное направление к площади поперечного сечения витков катушек. Поэтому увеличение угла между осями катушек индуктивности также уменьшает величину взаимной индуктивности.

Степень индуктивной связи двух катушек индуктивности характеризуют коэффициентом связи, представляющим собой среднее геометрическое отношений потокосцеплений взаимной индукции к полным потокам катушек,

Отсюда следует, что

Рассмотрим выражение

После замены в нём квадратного корня на взаимную индуктивность с учётом формулы (12.8) получаем строгие неравенства

и

Последнее соотношение позволяет проверять экспериментально полученные значения вза­имной индукции.

При изменении потока одной катушки, например, в первой, будет изменяться его потокосцепление с другой катушкой. Поэтому во второй катушке индуктивности, несмотря на то, что через неё не протекает ток, возникнет эдс взаимоиндукции величиной:

Аналогично может быть записано выражение эдс взаимной индукции, возникающей в первой катушке индуктивности при изменении магнитного потока второй катушки

Поэтому полные эдс взаимосвязанных катушек индуктивности с учётом выражения (12.6) могут быть записаны в виде