Тема: Эквивалентные преобразования формул логики первого порядка. Получение ПНФ, ССФ. Метод резолюций
В данной теме рассмотрим эквивалентные преобразования формул логики первого порядка, законы логики первого порядка, алгоритмы преобразования формул в предваренную нормальную форму и скулемовскую стандартную форму, доказательство логических следствий в ЛППП.
В логике высказываний были введены две нормальные формы ¾ конъюнктивная нормальная форма и дизъюнктивная нормальная форма. В логике первого порядка также имеется нормальная форма, называемая “предваренной нормальной формой” (ПНФ). Цель рассмотрения предваренной нормальной формы - упрощение процедуры доказательства. Формула F в логике первого порядка находится в предваренной нормальной форме тогда и только тогда, когда формула F имеет вид
(Q1х1)...(Qnxn)(M),
где каждое (Qixi), i=1,...,n, есть или ("xi) или ($xi), и М есть формула, не содержащая кванторов. (Q1х1)...(Qnxn) называется префиксом, а М-матрицей формулы F. Примеры формул находящихся в ПНФ:
("x)("y)(Р(х,у) Ù Q(y)),
 ("x)("y)($z)(Q(x,y)
("x)("y)($z)(Q(x,y) R(z)).
R(z)).
Для приведения формул к ПНФ важно понятие эквивалентности формул.
Две формулы F и G эквивалентны (F=G) тогда и только тогда, когда истинностные значения F и G одни и те же при любой интерпретации.
Основные пары эквивалентных формул, представляющие собой законы ЛВ, эквивалентны и в логике первого порядка. Кроме них существуют и другие пары эквивалентных формул, содержащих кванторы. Это следующие тождества, называемые законами логики первого порядка для кванторов:
1) Закон замены связанных переменных
("x)Р(х)=( "y)Р(у),
($x)Р(х)=( $y)Р(у).
Вводя новые обозначения для связанных переменных, следует выбрать букву, которая отсутствует в формуле, чтобы избежать так называемой коллизии переменных, т.е.:
("x)($y)Р(х,у)=("x)($z)Р(х,z), но
("x)($y)Р(х,у) ("x)($x)Р(х,х).
("x)($x)Р(х,х).
2) Коммутативные свойства кванторов
("x)( "y)Р(х,у)=("y)("x)Р(х,у),
($x)( $y)Р(х,у)=($y)($x)Р(х,у).
Необходимо помнить, что одноименные кванторы можно менять местами, а разноименные нельзя, т.е.
("x)($ y)Р(х,у) ¹ ($y)("x)Р(х,у).
3) Дистрибутивные свойства кванторов
("x)Р(х)ÚG=("x)(P(x) ÚG),
("x)Р(х)ÙG=("x)(P(x) ÙG),
($x)Р(х) ÚG=($x)(P(x) ÚG),
($x)Р(х) ÙG=($x)(P(x) ÙG),
где G - формула, не содержащая переменной х.
("x)Р(х) Ù( "x)Q(x)=("x)(P(x) ÙQ(x)),
($x)Р(х) Ú($x)Q(x)=($x)(P(x)ÚQ(x)),
т.е. квантор всеобщности " и квантор существования $ можно распределять по Ù и Ú соответственно. Однако квантор всеобщности " и квантор существования $ нельзя распределять по Ú и Ù соответственно, т.е.
("x)Р(х)Ú("x)Q(x) ¹ ("x)(P(x)ÚQ(x)),
($x)Р(х)Ù($x)Q(x) ¹ ($x)(P(x)ÙQ(x)).
В случаях подобных этим используют следующие тождества:
("x)F(x)Ú("x)Q(x)=("x)F(х)Ú("y)Q(y) = ("x)("y)(F(x)ÚQ(y)),
($x)F(x) Ù ($x)Q(x)=($x)F(х)Ù($y)Q(y) = ($x)($y)(F(x)ÙQ(y)).
4) Законы де Моргана для кванторов
Ø("x)Р(х)=( $x)ØР(х),
Ø($x)Р(х)=("x)ØР(х).
Процедура преобразования прозвольной формулы логики первого порядка в ПНФ осуществляется по следующему алгоритму:
Шаг 1. Используем законы
F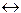 G=(F
G=(F G)(G
G)(G F),
F),
F G=FG,
G=FG,
чтобы исключить логические связки 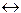 и
и  .
.
Шаг 2. Повторно используем закон
ØØ(F)=F,
законы де Моргана
Ø(FÚG)= ØFÙØG,
Ø (FÙG)= ØFÚØG
и законы
Ø (("x)F(x))=($x) ØF(x),
Ø (($x)F(x))=("x) ØF(x),
чтобы подвести знаки отрицания к предикатным символам.
Шаг 3. Переименовываем связанные переменные, если это необходимо.
Шаг 4. Используем законы
(Qx)F(x)ÚG=(Qx)(F(x)ÚG),
(Qx)F(x)ÙG=(Qx)(F(x)ÙG),
(где (Qх) есть "или или $)
("x)F(x)Ù ("x)H(x)=( "x)(F(x)ÙH(x)),
($x)F(x) Ú ($x)H(x)=($x)(F(x)ÚH(x)),
("x)F(x) Ú ("x)H(x)=( "x)( "y)(F(x)ÚH(y)),
($x)F(x)Ù ($x)H(x)=($x)($y)(F(x)ÙH(y)),
чтобы вынести кванторы в самое начало формулы для получения ПНФ.
Рассмотрим примеры решения типичных упражнений и задач по теме:
1. Привести формулу ("x)Р(х) ($x)Q(x) к ПНФ.
($x)Q(x) к ПНФ.
Решение.
("x)P(x) ($x)Q(x) = Ø(("x)P(x)) Ú ( $x)Q(x)=
($x)Q(x) = Ø(("x)P(x)) Ú ( $x)Q(x)=
($x) ØP(x) Ú($x)Q(x)=($x)(ØP(x)ÚQ(x)).
Следовательно, предваренная нормальная форма формулы ("x)P(x)®($x)Q(x) - это ($x)(ØP(x)ÚQ(x)).
2. Получить ПНФ для формулы
("x)("y)(($z)(P(x,z)ÙP(y,z)) ( $u)Q(x,y,u)).
( $u)Q(x,y,u)).
Решение.
("x)( "y)(($z)(P(x,z)ÙP(y,z)) ( $u)Q(x,y,u))=
( $u)Q(x,y,u))=
=("x)( "y)(Ø ($z)(Px,z) ÙP(y,z)) Ú($u)Q(x,y,u))=
=("x)("y)(("z)(ØP(x,z) Ú ØP(y,z)) Ú ( $u)Q(x,y,u))=
=("x)( "y)( "z)( $u)( ØP(x,z) Ú ØP(y,z) ÚQ(x,y,u)).
Следовательно, последняя формула есть ПНФ первой.
3. Покажем приложение логики первого порядка к решению задач. Пусть даны две аксиомы
А1: ("x)(ЧЕЛОВЕК(х) СМЕРТЕН(х)).
СМЕРТЕН(х)).
А2: ЧЕЛОВЕК(Конфуций).
Из А1 и А2 получить, что Конфуций смертен, т.е. показать, что СМЕРТЕН(Конфуций) есть логическое следствие А1 и А2.
Доказательство. Мы имеем
А1ÙА2: ("x)(ЧЕЛОВЕК(х) СМЕРТЕН(х)) ÙЧЕЛОВЕК(Конфуций).
СМЕРТЕН(х)) ÙЧЕЛОВЕК(Конфуций).
Если А1ÙА2 истинна в интерпретации I, то обе формулы А1 и А2 истинны в I. Так как (ЧЕЛОВЕК(х) СМЕРТЕН(х)) истинна для всех х, то, когда х заменяется на “Конфуций”, (ЧЕЛОВЕК(Конфуций)
СМЕРТЕН(х)) истинна для всех х, то, когда х заменяется на “Конфуций”, (ЧЕЛОВЕК(Конфуций) СМЕРТЕН(Конфуций)) истинна в I, т.е. ØЧЕЛОВЕК(Конфуций)ÚСМЕРТЕН(Конфуций) истинна в I. Однако ØЧЕЛОВЕК(Конфуций) ложна в I. Следовательно, СМЕРТЕН(Конфуций) должна быть истинной в I. Следовательно, мы показали, что СМЕРТЕН(Конфуций) истинна в I, если (А1ÙА2) истинна в I. По определению СМЕРТЕН(Конфуций) есть логическое следствие А1 и А2.
СМЕРТЕН(Конфуций)) истинна в I, т.е. ØЧЕЛОВЕК(Конфуций)ÚСМЕРТЕН(Конфуций) истинна в I. Однако ØЧЕЛОВЕК(Конфуций) ложна в I. Следовательно, СМЕРТЕН(Конфуций) должна быть истинной в I. Следовательно, мы показали, что СМЕРТЕН(Конфуций) истинна в I, если (А1ÙА2) истинна в I. По определению СМЕРТЕН(Конфуций) есть логическое следствие А1 и А2.
Контрольные вопросы и задания по теме:
1. Определение ПНФ.
2. Эквивалентность формул в логике первого порядка.
3. Законы логики первого порядка. Доказательство.
4. Тождества для кванторов. Доказательство.
5. Алгоритм преобразования формул логики первого порядка в ПНФ.
6. Преобразовать следующие формулы в ПНФ:
6.1. ("x)(P(x) ($y)Q(x,y));
($y)Q(x,y));
6.2. ($x)(Ø (($y)P(x,y) (($z)Q(z)
(($z)Q(z) R(x)));
R(x)));
6.3. ("x)("y)(($z)P(x,y,z)Ù (($u)Q(x,u) ($v)(y,v))).
($v)(y,v))).
7. Даны следующие утверждения:
F1: Каждый студент честен.
F2: Джон нечестен.
Из утверждений F1 и F2 получить, что Джон не студент.
#Тема: Скулемовские стандартные формы. Доказательство логических следствий в логике первого порядка
Рассмотрим преобразование формул логики первого порядка в скулемовскую стандартную форму, а также процедуру доказательства логических следствий в логике первого порядка с помощью метода резолюций.
Мы уже рассмотрели процедуры решения задач в ЛВ и логике первого порядка путем доказательства теорем. Однако чрезвычайно важны вопросы, связанные с поиском этих доказательств. Наиболее широко используются в настоящее время методы поиска доказательства теорем, предложенные Эрбраном в 1930 г. и Робинсоном в 1965 г. (метод резолюций). Общим для этих процедур является то, что они доказывают опровержение формулы, т.е. вместо общезначимости исходной формулы доказывают противоречивость ее отрицания. Эти процедуры применяются к формулам, представленным в так называемой скулемовской стандартной форме (ССФ).
Основные идеи ССФ :
1) Любая формула логики первого порядка может быть сведена к ПНФ, в которой матрица не содержит никаких кванторов, а префикс есть последовательность кванторов.
2) Поскольку матрица не содержит кванторов, она может быть сведена к КНФ.
3) Сохраняя противоречивость формулы, в ней можно элиминировать кванторы существования путем использования скулемовских функций.
Формула F имеет вид:
(Q1x1)(Q2x2)...(Qnxn)M, где M есть КНФ.
Положим Qr есть квантор существования в префиксе (Q1x1)(Q2x2)...(Qnxn),  . Тогда алгоритм перехода от ПНФ к ССФ описывается следующей последовательностью шагов:
. Тогда алгоритм перехода от ПНФ к ССФ описывается следующей последовательностью шагов:
1) Если никакой квантор  не стоит в префиксе левее Qr, выбираем новую константу с, отличную от других констант, входящих в М, заменяем все вхождения xr, встречающиеся в М, на с и вычеркиваем (Qrxr) из префикса.
не стоит в префиксе левее Qr, выбираем новую константу с, отличную от других констант, входящих в М, заменяем все вхождения xr, встречающиеся в М, на с и вычеркиваем (Qrxr) из префикса.
2) Если Qs ... Qs - список всех кванторов  , встречающихся левее Qr,
, встречающихся левее Qr,  , выбираем новый m-местный функциональный символ f, отличный от других функциональных символов, заменяем все xr в М на
, выбираем новый m-местный функциональный символ f, отличный от других функциональных символов, заменяем все xr в М на  и вычеркиваем (Qrxr) из префикса.
и вычеркиваем (Qrxr) из префикса.
3) Шаги 1 и 2 применяем ко всем кванторам  в префиксе. Последняя из полученных формул есть скулемовская стандартная форма или просто стандартная форма формулы F. Константы и функции, используемые для замены переменных квантора существования, называются скулемовскими функциями.
в префиксе. Последняя из полученных формул есть скулемовская стандартная форма или просто стандартная форма формулы F. Константы и функции, используемые для замены переменных квантора существования, называются скулемовскими функциями.
Необходимо также знать следующие определения. Дизъюнкт есть дизъюнкция литер. Иногда в целях удобства дизъюнкт обозначают как множество литер. Например,  . Дизъюнкт, содержащий r литер, называется r-литерным дизъюнктом. Однолитерный дизъюнкт называется единичным дизъюнктом. Дизъюнкт не содержащий никаких литер, называется пустым дизъюнктом. Пустой дизъюнкт всегда ложен, будем обозначать его Л. Считают, что множество дизъюнктов S есть конъюнкция всех дизъюнктов из S, где каждая переменная в S считается управляемой квантором всеобщности. Благодаря этому соглашению ССФ может быть просто представлена множеством дизъюнктов. Ранее упоминалось, что можно элиминировать (устранить) кванторы существования, сохраняя противоречивость формулы. Это утверждение доказывается в следующей теореме.
. Дизъюнкт, содержащий r литер, называется r-литерным дизъюнктом. Однолитерный дизъюнкт называется единичным дизъюнктом. Дизъюнкт не содержащий никаких литер, называется пустым дизъюнктом. Пустой дизъюнкт всегда ложен, будем обозначать его Л. Считают, что множество дизъюнктов S есть конъюнкция всех дизъюнктов из S, где каждая переменная в S считается управляемой квантором всеобщности. Благодаря этому соглашению ССФ может быть просто представлена множеством дизъюнктов. Ранее упоминалось, что можно элиминировать (устранить) кванторы существования, сохраняя противоречивость формулы. Это утверждение доказывается в следующей теореме.
Теорема 3. Пусть S - множество дизъюнктов, которые представляют ССФ формулы F. Тогда F противоречива в том и только в том случае, когда S противоречива. Необходимо знать доказательство этой теоремы (см.[7,с.55-58]). Отметим, что формула может иметь более чем одну стандартную форму. Для простоты при преобразовании формулы F в стандартную форму S стараются заменять кванторы  скулемовскими функциями настолько простыми, насколько возможно. Тогда для формулы
скулемовскими функциями настолько простыми, насколько возможно. Тогда для формулы  можно отдельно получить множество дизъюнктов Si, где каждый Si представляет стандартную форму Fi, i=1,...,n. Затем допускаем, что
можно отдельно получить множество дизъюнктов Si, где каждый Si представляет стандартную форму Fi, i=1,...,n. Затем допускаем, что  . Опираясь на теорему 3, можно доказать что F противоречива тогда и только тогда, когда S противоречива. В дальнейшем для доказательства теорем будем использовать процедуру опровержения. На входе процедуры опровержения всегда стоит множество дизъюнктов S. Для множества дизъюнктов используют термины “невыполнимо” (“выполнимо”) вместо “противоречиво” (“непротиворечиво”).
. Опираясь на теорему 3, можно доказать что F противоречива тогда и только тогда, когда S противоречива. В дальнейшем для доказательства теорем будем использовать процедуру опровержения. На входе процедуры опровержения всегда стоит множество дизъюнктов S. Для множества дизъюнктов используют термины “невыполнимо” (“выполнимо”) вместо “противоречиво” (“непротиворечиво”).
Одной из наиболее эффективных процедур поиска опровержения формулы является метод резолюций. Основная идея метода резолюций состоит в том, чтобы проверить, содержит ли S пустой дизъюнкт Л. Если S содержит Л, то S невыполнимо. Если S не содержит Л, то проверяется следующий факт: можно ли получить Л из S. Действительно, множество дизъюнктов невыполнимо тогда и только тогда, когда пустой дизъюнкт Л является логическим следствием этого множества:
 Л,
Л,
(Выражения  обозначают соответственно “А дает В”; “А тогда и только тогда, когда В”). Таким образом, невыполнимость множества дизъюнктов S можно доказать порождением логических выводов из S до тех пор, пока не получим пустой дизъюнкт Л.
обозначают соответственно “А дает В”; “А тогда и только тогда, когда В”). Таким образом, невыполнимость множества дизъюнктов S можно доказать порождением логических выводов из S до тех пор, пока не получим пустой дизъюнкт Л.
Для порождения логических следствий используется такая схема. Пусть A, B, X - формулы и пусть  и
и  истинны одновременно. Тогда имеем: если X истинно, то В также должно быть истинным. Если Х ложно, то обязательно А истинно, т.е. формула
истинны одновременно. Тогда имеем: если X истинно, то В также должно быть истинным. Если Х ложно, то обязательно А истинно, т.е. формула  обязательно истинна. Тогда выполняется следующее правило:
обязательно истинна. Тогда выполняется следующее правило:
 .
.
Это правило можно записать иначе:
 ,
,
где Х-высказывание, представленное литерой в логике высказываний или предикатным символом; А и В - дизъюнкты. Данное правило известно как правило резолюций. Справедливость его можно установить, например, воспользовавшись Теоремой 1, т.е.
Если  , то
, то  И.
И.
Имеет место Лемма 1: Пусть S1 и S2 - дизъюнкты некоторой КНФ, обозначенной S, и пусть L-литера. Если  , то дизъюнкт
, то дизъюнкт

является логическим следствием нормальной формы S.
Следствие Леммы 1: Нормальная форма S и формула  эквивалентны. Дизъюнкт r называется резольвентой дизъюнктов S1 и S2. Литеры L и
эквивалентны. Дизъюнкт r называется резольвентой дизъюнктов S1 и S2. Литеры L и  называются контрарными.
называются контрарными.
Обобщенный алгоритм доказательства невыполнимости конечного множества дизъюнктов S, при условии, что Л состоит из последовательности шагов:
состоит из последовательности шагов:
1) Выбираем дизъюнкты S1, S2 и литеру L такую, что  , и получаем резольвенту r.
, и получаем резольвенту r.
2) Добавляем r в множество S и получаем
1)  .
.
Шаги (1) и (2) повторяются до тех пор, пока не будет получен пустой дизъюнкт Л.
Необходимо знать следующие определения. Пусть S-множество дизъюнктов. Резолютивный вывод C из S есть такая конечная последовательность C1, C2,..., Ck дизъюнктов, что каждый Ci или принадлежит S или является резольвентой дизъюнктов, предшествующих Ci, и Ck = C. Вывод Л из S называется опровержением (или доказательством невыполнимости) S.
При использовании метода резолюций для логики первого порядка необходимо обратить внимание на следующие особенности. Существенным моментом в применении правила резолюции является нахождение в дизъюнкте литеры, которая контрарна литере в другом дизъюнкте. Для дизъюнктов, не содержащих переменных, это просто. Если же дизъюнкты содержат переменные, процедура доказательства усложняется. В этом случае предварительно должна быть проведена некоторая подстановка в переменные и введено понятие унификации с помощью этой подстановки. Например, рассмотрим предикаты L(x) и L(a), где x -переменная, a - константа. В этих предикатах предикатные символы одинаковы, чего нельзя сказать о самих предикатах. Тем не менее, подстановкой a в x можно эти предикаты сделать одинаковыми (эта подстановка называется унификацией). Целью унификации является обеспечение возможности применения алгоритма доказательства методом резолюций для предикатов. Например, если имеем:

то предикаты L(x) и  не являются контрарными. При подстановке a вместо x получим L(a) и
не являются контрарными. При подстановке a вместо x получим L(a) и  , т.е. контрарную пару. Подстановку t в x принято записывать {t|x}. В общем случае подстановка - это конечное множество вида {t1|v1, t2|v2, ... , tn|vn}, где каждое vi - переменная, каждое ti - терм (константа, переменная, символ функции), отличный от vi, причем все vi разные.
, т.е. контрарную пару. Подстановку t в x принято записывать {t|x}. В общем случае подстановка - это конечное множество вида {t1|v1, t2|v2, ... , tn|vn}, где каждое vi - переменная, каждое ti - терм (константа, переменная, символ функции), отличный от vi, причем все vi разные.
Пусть q={t1|v1, t2|v2, ... , tn|vn} - подстановка, E - выражение. Тогда Eq - выражение, полученное из E заменой одновременно всех вхождений переменной vi ( ) в E на терм ti, Eq называется примером E.
) в E на терм ti, Eq называется примером E.
Например, пусть q ={a|x, f(b)|y, c|z} и E=P(x, y, z). Тогда Eq =P(a, f(b), c). Подстановка q называется унификатором для множества {E1,E2,...,Ek} тогда и только тогда, когда E1q=E2q=...= Ekq. Говорят, что множество {E1,...,Ek} унифицируемо, если для него существует унификатор. Например, множество {P(a, y), P(x, f(b))} унифицируемо, т.к. подстановка q={a|x, f(b)|y} является его унификатором.
Рассмотрим примеры решения типичных упражнений и задач:
1. Получить ССФ формулы ($x)("y)("z)($u)("v)($w)P(x,y,z,u,v,w).
Решение. Данная формула находится в предваренной нормальной форме. Воспользуемся алгоритмом перехода от ПНФ к скулемовской стандартной форме. В данной формуле левее ($x) нет никаких кванторов всеобщности, левее ($u) стоят ("y) и ("z), а левее ($w) стоят ("y), ("z) и ("v). Следовательно, мы можем заменить переменную x на константу a, переменную u - на двухместную функцию f(y,z), переменную w - на трехместную функцию g(y,z,v). Таким образом, получаем следующую стандартную форму для заданной формулы:
("y)("z)("v)P(a,y,z,f(y,z),g(y,z,v)).
2. Получить ССФ для формулы
("x)($y)($z)((ùP(x,y)ÙQ(x,z))ÚR(x,y,z)).
Решение. Сначала приведем матрицу к КНФ:
("x)($y)($z)((ùP(x,y)ÚR(x,y,z))Ù(Q(x,z)ÚR(x,y,z))).
Затем, т.к. перед ($y) и ($z) есть ("x), то переменные y и z заменяются соответственно одноместными функциями f(x) и g(x). Таким образом, получаем следующую ССФ:
("x)((ùP(x,f(x))ÚR(x,f(x),g(x)))Ù(Q(x,g(x))ÚR(x,f(x),g(x)))).
3. Пусть S - ССФ формулы F. Если F противоречива, то по Теореме 3 F=S. Если F непротиворечива, то, вообще говоря, F не эквивалентна S. Доказать это утверждение.
Доказательство. Пусть, например,  . Ясно, что S есть стандартная форма формулы F. Выберем интерпретацию I следующим образом:
. Ясно, что S есть стандартная форма формулы F. Выберем интерпретацию I следующим образом:
Область: D={1,2}.
Значения для a:
| a |
Значения для P:
| P(1) | P(2) |
Тогда ясно, что F истинна в I, поскольку P(x) ¹ Þ ($x)P(x)=1. Однако S ложна в I, поскольку a=1ÞP(a)=P(1)=0. Таким образом, F¹S.
4. Проверить невыполнимость множества дизъюнктов
{PÚQ, PÚR, ùQÚùR, ùP}.
Решение. Используем метод резолюций. Выпишем исходное множество дизъюнктов:

Алгоритм проверки невыполнимости в общем случае не детерминирован. Мы можем выбирать S1, S2 и L разными способами. Например, если выбирать дизъюнкты в лексикографическом порядке возрастания их номеров, получим следующую последовательность вывода:
(5) PÚùR (из 1 и 3),
(6) Q (из 1 и 4),
(7) PÚùQ (из 2 и 3),
(8) R (из 2 и 4),
(9) P (из 2 и 5),
(10) ùR (из 3 и 6),
(11) ùQ (из 3 и 8),
(12) ùR (из 4 и 5),
(13) ùQ (из 4 и 7),
(14) Л (из 4 и 9).
Как видим, выбранная стратегия не оптимальна. Некоторые резольвенты лишние. Для сравнения покажем действие этого же алгоритма с минимальным количеством резолюций:
(5) Q (из 1 и 4),
(6) R (из 2 и 4),
(7) ùQ (из 3 и 6),
(8) Л (из 5 и 7).
Ясно, что выбранная стратегия может значительно влиять на выполнение алгоритма. Отметим два важных свойства алгоритма, не зависящих от выбранной стратегии: 1) Если множество S не содержит дизъюнктов, к которым можно применить схему резолюций, то оно выполнимо, за исключением тех случаев, когда это множество содержит пустой дизъюнкт. Интерпретация I получается заданием атома P=1 тогда и только тогда, когда P присутствует в формуле без отрицания. Например: (1) PÚùS, (2) PÚùD. При интерпретации P=1, S=0, D=0 (PÚùS)Ù(PÚùD)=1; 2) Если алгоритм закончил работу после порождения пустого дизъюнкта, то установлена невыполнимость исходного множества дизъюнктов S.
5. Проверить невыполнимость множества дизъюнктов
S={P Q, ùP
Q, ùP Q, P
Q, P ùQ, ùPÚùQ}.
ùQ, ùPÚùQ}.
Решение.

(5) Q (из 1 и 2),
(6) ùQ (из 3 и 4),
(7) Л (из 5 и 6).
Т.к. получен ложный дизъюнкт Л, то S невыполнимо. Указанный вывод представлен деревом на рис.6.1, которое называется деревом вывода:
 PÚQ ùPÚQ PÚùQ ùPÚùQ
PÚQ ùPÚQ PÚùQ ùPÚùQ
Q ùQ
Л
Рисунок 6.1
6. Дано следующее множество формул:
F1: ("x)(C(x)®(W(x)ÙR(x))),
F2: ($x)(C(x)ÙO(x)),
G : ($x)(O(x)ÙR(x)).
Доказать, что G является логическим следствием F1 и F2.
Решение. Преобразуем F1, F2 и ùG в стандартную форму. В результате получим следующие пять дизъюнктов:


(5) ùO(x)ÚùR(x) из ùG.
Это множество дизъюнктов невыполнимо. Это можно доказать при помощи метода резолюций следующим образом. Применив подстановку q={a|x} к данному множеству дизъюнктов, получим:
(1) ùC(a)ÚW(a),
(2) ùC(a)ÚR(a),
(3) C(a),
(4) O(a),
(5) ùO(a)ÚùR(a).
(6) R(a) резольвента (3) и (2),
(7) ùR(a) резольвента (5) и (4),
(8) Л резольвента (7) и (6).
Таким образом, G - логическое следствие F1 и F2.
Контрольные вопросы и задания:
1. Определение ССФ. Алгоритм преобразования поизвольной формулы F логики первого порядка в ССФ.
2. Множество дизъюнктов. Определение r-литерного, единичного и пустого дизъюнктов.
3. Теорема 3 о противоречивости произвольной формулы F логики первого порядка и ее ССФ. Формулировка и доказательство.
4. Основная идея метода резолюций.
5. Резольвента. Лемма 1 о логическом следствии нормальной
формы S.
6. Доказательство невыполнимости, основанное на принципе резолюций.
7. Метод резолюций для получения логических следствий в логике высказываний.
8. Особенности метода резолюций в логике первого порядка.
9. Унификация тернов. Стратегии вывода.
10. Найти ССФ для каждой из формул:
10.1. ù(("x)P(x)®($y)("z)Q(y,z));
10.2. ("x)((ùE(x,0)®(($y)(E(y,g(x))Ù("z)(E(z,g(x))®E(y,z)))));
10.3. ù(("x)P(x)®($y)P(y).
11. Доказать невыполнимость множества дизъюнктов методом резолюций S={H, ùHÚPÚQ, ùPÚC, ùQÚC, ùC}.
12. Даны утверждения:
(1) P®S,
(2) S®U,
(3) P,
(4) U.
Доказать, используя метод резолюций, что (4) следует из (1), (2), (3).
13. Даны формулы:
F1: (P®(ùQÚ(RÙS))),
F2: P,
F3: ùS,
G : ùQ.
Выяснить используя метод резолюций, является ли G логическим следствием F1,F2,F3.
14. Для формул
F1: ($x)(P(x)Ù("y)(D(y)®L(x,y))),
F2: ("x)(P(x)®("y)(Q(y)®ùL(x,y))),
G : ("x)(D(x)®ùQ(x)
доказать, что G является логическим следствием F1 и F2, используя метод резолюций.
15. Пусть q={a|x,b|y,g(x,y)|z} - подстановка, и E=P(h(x,y)). Найти Eq.
16. С помощью резолюций докажите, что (ùQ®ùP) есть логическое следствие (P®Q).
17. Пусть S={ùPÚùQÚR, PÚR, QÚR, ùR}. Доказать противоречивость множества S, используя метод резолюций.