Интерпретации формул логики первого порядка
Рассмотрим приемы формализации естественно-языковых высказываний средствами логики первого порядка, а также способы определения истинностных значений формул логики первого порядка при заданных интерпретациях.
В логике высказываний атом представляет собой повествовательное предложение, которое может быть или истинно, или ложно, но не то и другое вместе. Атом рассматривается как единое целое. Его структура и состав не анализируются.
Однако есть много умозаключений, которые не могут быть рассмотрены таким простым способом. Поэтому вводится логика первого порядка (логика предикатов), которая по сравнению с логикой высказываний имеет еще три логических понятия: термы, предикаты и кванторы. Большая часть повседневного и математического языка может быть формализована логикой 1-го порядка. Предикат ¾ это двухзначная функция вида Р(х1,...,хn) = у, аргументы которой определены в произвольном множестве М, называемом предметной областью, т.е. х1,...,хnÎМ={a1,...,am}, yÎ{0,1}, a1,...,am ¾ предметы. Задать предикат ¾ значит указать предметную область для каждой предметной переменной, а также значение предиката для каждого из возможных наборов значений аргументов.
Для построения атомов логики первого порядка используются следующие четыре типа символов:
1) Индивидные символы или константы. Это обычно имена объектов, такие как Джон, 3.
2) Символы предметных переменных. Это обычно строчные буквы x,y,z,..., возможно с индексами.
3) Функциональные символы. Это обычно строчные буквы f,g,h,... или осмысленные слова из строчных букв, такие как “плюс”, “отец”, и т.д.
4) Предикатные символы. Это обычно прописные буквы P,Q,R,... или осмысленные слова из прописных букв, такие как БОЛЬШЕ или ЛЮБИТ.
Всякая функция или предикатный символ имеет определенное число аргументов. Если функциональный символ f имеет n аргументов, то f называется n-местным функциональным символом. Индивидный символ или константа может рассматриваться как функциональный символ без аргументов. Аналогично, если предикатный символ Р имеет n аргументов, то Р называется n-местным предикатным символом. Например, нам нужно представить высказывание “х больше 3”. Сначала определим двухместный предикат БОЛЬШЕ (х,у), который означает “х больше у”. Тогда высказывание “х больше 3” представляется выражением БОЛЬШЕ (х,3). Данный предикат задает бинарное отношение, т.е. множество пар, в которых первое число больше 3. Отметим, что предикат определяется как функция, принимающая значение 1 (истина) на наборах, удовлетворяющих заданному отношению v, и принимающая значение 0 (ложь) на наборах не удовлетворяющих v. Аналогично высказывание “х
любит у” можно представить с помощью предиката ЛЮБИТ(х,у). Для обозначения высказываний “х+у” и “Отец человека х” можно использовать функциональные символы плюс(х,у) и отец(х). Предложения “х+1 больше х” и “Отец Джона любит Джона” можно символически представить в виде БОЛЬШЕ(плюс(х,1),х) и ЛЮБИТ(отец(Джон), Джон).
В логике первого порядка термы определяются рекурсивно следующим образом:
1) Константа есть терм.
2) Переменная есть терм.
3) Если F есть n-местный функциональный символ и t1,...,tn ¾ термы, то F(t1,...,tn) ¾ терм. Никаких термов, кроме порожденных применением указанных правил (1-3) нет. Например, т.к. х и 1 ¾ термы и плюс ¾ двухместный функциональный символ, то плюс(х,1) есть терм.
Предикат есть отображение, которое отображает список констант в И или Л. Например, БОЛЬШЕ есть предикат. БОЛЬШЕ(5,3) есть И, но БОЛЬШЕ(1,3) есть Л. Если Р ¾ n-местный предикатный символ и t1,...,tn- термы, то Р(t1,...,tn) ¾ атом. В логике первого порядка, как и в логике высказываний, вводятся пять логических связок для построения формул:  . Вводятся также два специальных символа " и $, чтобы характеризовать переменные. " ¾ квантор всеобщности. Если х ¾ переменная, то ("x) читается как “для всех х”, “для каждого х” или “для всякого х”. $ ¾ квантор существования, ($x) читается “существует х”, “для некоторых х” или “ по крайней мере для одного х”. ("x) и ($x) называют кванторными комплексами. Область действия квантора ¾ та формула, к которой он применяется. Например, область действия квантора существования в формуле ("x)($y)МЕНЬШЕ(х,у) есть МЕНЬШЕ(х,у), а область действия квантора всеобщности ¾ формула ($y)МЕНЬШЕ(х,у). Область действия в кванторе ("x)(Q(x)
. Вводятся также два специальных символа " и $, чтобы характеризовать переменные. " ¾ квантор всеобщности. Если х ¾ переменная, то ("x) читается как “для всех х”, “для каждого х” или “для всякого х”. $ ¾ квантор существования, ($x) читается “существует х”, “для некоторых х” или “ по крайней мере для одного х”. ("x) и ($x) называют кванторными комплексами. Область действия квантора ¾ та формула, к которой он применяется. Например, область действия квантора существования в формуле ("x)($y)МЕНЬШЕ(х,у) есть МЕНЬШЕ(х,у), а область действия квантора всеобщности ¾ формула ($y)МЕНЬШЕ(х,у). Область действия в кванторе ("x)(Q(x) R(x)) есть (Q(x)
R(x)) есть (Q(x) R(x)).
R(x)).
Вхождение переменной х в формулу называется связанным тогда и только тогда, когда оно совпадает с вхождением в кванторный комплекс ("x) или ($x) или находится в области действия такого комплекса. Вхождение переменной в формулу свободно тогда и только тогда, когда оно не является связанным. Переменная свободна в формуле, если
хотя бы одно ее вхождение в эту формулу свободно. Переменная связана в формуле, если хотя бы одно ее вхождение в эту формулу связано. В формуле ("x)Р(х,у) переменная х связана, так как оба вхождения х связаны. Однако переменная у свободна, так как единственное вхождение у свободно. Переменная в формуле может быть свободной и связанной одновременно. Например, у и свободна и связана в формуле ("x)Р(х,у)Ù("y)Q(у).
Правильно построенные формулы (ППФ) или, короче, формулы логики первого порядка рекурсивно определяются следующим образом:
1) Атом есть формула. (Отметим, что “атом” ¾ сокращение для атомарной формулы).
2) Если F и G формулы, то Ø(F), (FÚG), (FÙG), (F G) и (F
G) и (F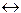 G) ¾ формулы.
G) ¾ формулы.
3) Если F ¾ формула, а х ¾ свободная переменная в F, то ("x)F и
($x)F ¾ формулы.
Формулы порождаются только конечным числом применений правил (1-3). В дальнейшем круглые скобки во всех формулах могут быть опущены в соответствии с соглашениями, которые были установлены в логике высказываний. (Пропозициональным или логическим связкам приписывается убывающий ранг в следующем порядке:  ). Расширим эти соглашения, считая, что кванторы имеют наименьший ранг. Например, ($x)AÚB обозначает ((($x)A)Ú(B)).
). Расширим эти соглашения, считая, что кванторы имеют наименьший ранг. Например, ($x)AÚB обозначает ((($x)A)Ú(B)).
В логике высказываний интерпретация есть приписывание атомам истинностных значений. Чтобы определить интерпретацию для формулы логики первого порядка, нужно указать предметную область (область значений предметных переменных) и значения констант, функциональных и предикатных символов, встречающихся в формуле. Интерпретация формулы F логики первого порядка состоит из непустой (предметной) области D и указания “оценки” (значения) всех констант, функциональных символов и предикатных символов, встречающихся в F.
1. Каждой константе ставят в соответствие некоторый элемент из D.
2. Каждому n-местному функциональному символу ставят в соответствие отображение из Dn в D. (Заметим, что Dn ={(x1,...,xn)|x1ÎD,...,xnÎD}).
3. Каждому n-местному предикатному символу ставят в соответствие отображение Dn в {И,Л} (или в {1,0}).
Для каждой интерпретации формулы на области D формула может получить истинное значение И или Л согласно следующим правилам:
1. Если заданы истинностные значения формул G и H, то истинностные значения формул ØG, (GÚH), (GÙH), (G H), (G
H), (G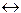 H) получаются с помощью таблицы 3.
H) получаются с помощью таблицы 3.
2. ("x)G получает значение 1, если G получает значение 1 для каждого х из D; в противном случае она получает значение 0.
("x)G(x)=
3. ($x)G получает значение 1, если G получает значение 1 хотя бы для одного х из D; в противном случае она получает значение 0.
($x)G(x)=
Кроме того, в логике первого порядка определяются следующие понятия. Формула G непротиворечива (выполнима) тогда и только тогда, когда существует такая интерпретация I, что G имеет значение 1 в I. Если формула G=1 в интерпретации I, то говорят, что I есть модель формулы G и I удовлетворяет G. Формула G противоречива (невыполнима) тогда и только тогда, когда не существует интерпретация, которая удовлетворяет G. Формула G общезначима тогда и только тогда, когда не существует никакой интерпретации, которая не удовлетворяет формуле G. Формула G есть логическое следствие формул F1,F2,...,Fn тогда и только тогда, когда для каждой интерпретации I, если F1Ù...ÙFn истинна в I, то G также истинна в I. Отношение между общезначимостью (противоречивостью) и логическим следствием, установленные в теоремах 1,2 логики высказываний (см. п.3.3) верны также и в логике первого порядка. В действительности логика первого порядка может рассматриваться как расширение логики высказываний. Поскольку в логике первого порядка имеется бесконечное число областей, то, вообще говоря, имеется бесконечное число интерпретаций формулы. Следовательно, в отличие от ЛВ, невозможно доказать общезначимость или противоречивость формулы оценкой формулы при всех возможных интерпретациях.
Рассмотрим примеры решения типичных упражнений и задач:
1. Записать следующие утверждения в виде формул логики первого порядка:
а) Каждое рациональное число есть вещественное число.
б) Существует число, которое является простым.
с) Для каждого числа х существует такое число у, что x<y.
Решение. Обозначим высказывание “х есть простое число” через Р(х), “х есть рациональное число” через Q(x), “х есть вещественное число” через R(x) и “х меньше у” через МЕНЬШЕ(х,у). Тогда указанные утверждения соответственно могут быть записаны:
a) ("x)(Q(x) R(x)),
R(x)),
b) ($y)P(у),
c) ("x)($y)МЕНЬШЕ(х,у).
2. Перевести утверждение “Каждый человек смертен. Конфуций ¾ человек. Следовательно, Конфуций смертен” в формулу.
Решение. Обозначим “х есть человек” через ЧЕЛОВЕК(х) и “х смертен” через СМЕРТЕН(х). Тогда утверждение “Каждый человек смертен” может быть представлено формулой ("x)(ЧЕЛОВЕК(х) СМЕРТЕН(х)), утверждение “Конфуций - человек” ¾ формулой ЧЕЛОВЕК(Конфуций) и “Конфуций смертен” ¾ формулой СМЕРТЕН(Конфуций). Утверждение в целом может быть представлено формулой
СМЕРТЕН(х)), утверждение “Конфуций - человек” ¾ формулой ЧЕЛОВЕК(Конфуций) и “Конфуций смертен” ¾ формулой СМЕРТЕН(Конфуций). Утверждение в целом может быть представлено формулой
("x)(ЧЕЛОВЕК(х) СМЕРТЕН(х)) Ù ЧЕЛОВЕК(Конфуций)
СМЕРТЕН(х)) Ù ЧЕЛОВЕК(Конфуций) СМЕРТЕН(Конфуций).
СМЕРТЕН(Конфуций).
3. Основные аксиомы натуральных чисел таковы:
А1: Для каждого числа существует одно и только одно число, непосредственно следующее за ним.
А2: Нет числа, за которым непосредственно следует 0.
А3: Для каждого числа, отличного от нуля, существует одно и только одно непосредственно предшествующее ему число.
Записать их в виде формул логики первого порядка.
Решение. Пусть f(х) и g(х) представляют соответственно число, непосредственно следующее за х и непосредственно предшествующее х. Пусть “х равно у” обозначается через Е(х,у). Тогда аксиомы могут быть представлены следующими формулами:
 1: ("x)($y)(E(y,f(x))Ù("z)(E(z,f(x))
1: ("x)($y)(E(y,f(x))Ù("z)(E(z,f(x)) E(y,z))),
E(y,z))),
 2: (($x)E(0,f(x))),
2: (($x)E(0,f(x))),
 3: ("x)(ùE(x,0)
3: ("x)(ùE(x,0) ($y)(E(y,g(x))Ù("z)(E(z,g(x))
($y)(E(y,g(x))Ù("z)(E(z,g(x)) E(y,z))))).
E(y,z))))).
4. Даны формулы ("x)Р(х) и ($x)ØР(х) и задана интерпретация: D={1,2}, оценка для Р такова:
| Р(1) | Р(2) |
Определить истинностные значение заданных формул.
Решение. Легко убедиться, что ("x)Р(х) ложна в этой интерпретации:
P(2)=0ÞP(x) 1Þ ("x)P(x)=0 по определению квантора всеобщности. (Þ- знак логического следования, обозначающий “из А следует В”). С другой стороны, ØР(2)=1 в этой интерпретации, т.е. имеем: ØР(2)=1ÞP(x)
1Þ ("x)P(x)=0 по определению квантора всеобщности. (Þ- знак логического следования, обозначающий “из А следует В”). С другой стороны, ØР(2)=1 в этой интерпретации, т.е. имеем: ØР(2)=1ÞP(x) 0Þ Þ($x)ØР(x)=1, ($x)ØР(x) есть истина в этой интерпретации.
0Þ Þ($x)ØР(x)=1, ($x)ØР(x) есть истина в этой интерпретации.
5. Для формулы ("x)($у)Р(х,у) задана интерпретация на области D={1,2}:
| Р(1,1) | Р(1,2) | Р(2,1) | Р(2,2) |
Определить истинностные значения.
Решение. Если х=1, то ($у)Р(1,у)=1, т.к. при у=1 имеем: Р(1,1)=1, следовательно, Р(1,у) 0Þ($у)Р(1,у)=1. Если х=2, то ($у)Р(2,у)=1, т.к. при у=2 имеем: Р(2,2)=1, следовательно, Р(2,2)
0Þ($у)Р(1,у)=1. Если х=2, то ($у)Р(2,у)=1, т.к. при у=2 имеем: Р(2,2)=1, следовательно, Р(2,2) 0Þ($у)Р(2,у)=1. Следовательно, в данной интерпретации для каждого х из D существует такой у, что Р(х,у)=1, т.е. ("x)($у)Р(х,у) истинна в этой интерпретации.
0Þ($у)Р(2,у)=1. Следовательно, в данной интерпретации для каждого х из D существует такой у, что Р(х,у)=1, т.е. ("x)($у)Р(х,у) истинна в этой интерпретации.
6. Пусть формула G: ("x)(P(х) Q(f(x),a)). В формуле G имеется: одна константа а; один одноместный функциональный символ f; один одноместный предикатный символ Р; один двухместный предикатный символ Q. Задана интерпретация I формулы G:
Q(f(x),a)). В формуле G имеется: одна константа а; один одноместный функциональный символ f; один одноместный предикатный символ Р; один двухместный предикатный символ Q. Задана интерпретация I формулы G:
Оценка для а:
| а |
Оценка для f:
| f(1) | f(2) |
Оценки для P и Q:
| P(1) | P(2) | Q(1,1) | Q(1,2) | Q(2,1) | Q(2,2) |
Определить истинностные значения G в заданной интерпретации.
Решение. Если х=1, то Р(х) Q(f(x),a)=P(1)
Q(f(x),a)=P(1) Q(f(1),a)==P(1)
Q(f(1),a)==P(1) Q(2,1)=0
Q(2,1)=0 0=1.Если х=2, то P(x)
0=1.Если х=2, то P(x) Q(f(x),a)=P(2)
Q(f(x),a)=P(2) Q(f(2),a)=P(2)
Q(f(2),a)=P(2) Q(1,1)=1
Q(1,1)=1 1=1.Поскольку Р(х)
1=1.Поскольку Р(х) Q(f(x), a) истинно для всех элементов х из области D,
Q(f(x), a) истинно для всех элементов х из области D,
то формула ("x)(P(х) Q(f(x),a)) истинна в интерпретации I.
Q(f(x),a)) истинна в интерпретации I.
7. Даны формулы
F1: ("x)(P(х) Q(x)),
Q(x)),
F2: P(a).
Доказать, что формула Q(a) есть логическое следствие формул F1 и F2.
Доказательство. Рассмотрим любую интерпретацию I, которая удовлетворяет ("x)(P(х) Q(x))ÙР(а). Ясно, что в этой интерпретации Р(а)=1. Пусть Q(a)
Q(x))ÙР(а). Ясно, что в этой интерпретации Р(а)=1. Пусть Q(a) 1 в этой интерпретации, тогда ØP(a)ÚQ(a)=P(a)
1 в этой интерпретации, тогда ØP(a)ÚQ(a)=P(a) Q(a)=0 в I. Это значит, что ("x)(P(х)
Q(a)=0 в I. Это значит, что ("x)(P(х) Q(x))=0 в I, что невозможно. Следовательно, Q(а) должна быть истинной в каждой интерпретации, которая удовлетворяет ("x)(P(х)
Q(x))=0 в I, что невозможно. Следовательно, Q(а) должна быть истинной в каждой интерпретации, которая удовлетворяет ("x)(P(х) Q(x))ÙР(а). Это значит, что Q(a) есть логическое следствие из F1 и F2.
Q(x))ÙР(а). Это значит, что Q(a) есть логическое следствие из F1 и F2.
Контрольные вопросы и задания по теме:
1. Атомы логики первого порядка.
2. Термы, n-местные предикаты.
3. Кванторные комплексы.
4. Свободная и связанная переменные в формулах логики первого порядка.
5. Правильно построенные формулы в логике первого порядка.
6. Интерпретация формулы логики первого порядка.
7. Противоречивость, непротиворечивость и общезначимость формул логики первого порядка.
8. Логическое следствие в логике первого порядка.
9. Для перечисленных формул доказать, что:
9.1. ("x)Р(х)Ù($x)ØР(у) противоречива;
9.2. ("x)Р(х) ($у)Р(у) общезначима;
($у)Р(у) общезначима;
9.3. Р(а) Ø(($x)Р(х)) непротиворечива;
Ø(($x)Р(х)) непротиворечива;
9.4. ("x)Р(х)Ú(($у)ØР(у)) общезначима.
10. Для следующей интерпретации (D={a,b}):
| P(a,a) | P(a,b) | P(b,a) | P(b,b) |
определить истинностные значения следующих формул:
10.1. ("x)($у)Р(х,у);
10.2. ("x)("y)Р(х,у);
10.3. ($x)("y)Р(х,у);
10.4. ($у)ØР(а,у);
10.5. ("x)("y)(Р(х,у) Р(у,х));
Р(у,х));
10.6. ("x)Р(х,х);
11. Дана формула А: ($x)Р(х) ("x)Р(х).
("x)Р(х).
11.1. Доказать, что эта формула всегда истинна, если область D содержит только один элемент.
11.2. Пусть D={a,b}. Найти интерпретацию с областью D, в которой А=0.
12. Задана следующая интерпретация:
Область: D={1,2}.
Значение констант а и b:
| a | b |
Значение функции f:
| f(1) | f(2) |
Значение предиката Р:
| Р(1,1) | P(1,2) | P(2,1) | P(2,2) |
Найти истинностные значения следующих формул в указанной интерпретации:
12.1. Р(а,f(a))ÙP(b,f(b));
12.2. ("x)($у)P(x,y);
12.3. ("x)("y)(P(x,y) P(f(x),f(y))).
P(f(x),f(y))).
13. Пусть F1 и F2 таковы: F1: ("x)(Р(х) Q(x)), F2: ØQ(a).
Q(x)), F2: ØQ(a).
Доказать, что ØP(a) есть логическое следствие F1 и F2.