Доказательство логических следствий в логике высказываний
Рассмотрим понятие логического вывода в логике высказываний и процедуры логического вывода.
Необходимо усвоить следующие основные понятия. В математике, как и в обычной жизни, часто нужно решить, следует ли одно утверждение из нескольких других. Это приводит к понятию “логический вывод”. Пусть даны формулы F1,F2,...,Fn и формула G. Товорят, что G есть логическое следствие формул F1,F2,...,Fn (или G логически следует из F1,F2,...,Fn) тогда и только тогда, когда для всякой интерпретации I, в которой F1ÙF2Ù...ÙFn истинна, G также истинна. F1,F2,...,Fn называются аксиомами (или постулатами или посылками) G.
Следует знать и уметь пользоваться следующими теоремами о выводе логического следствия:
Теорема 1. Пусть даны формулы F1,F2,...,Fn и формула G. Тогда G есть логическое следствие F1,F2,...,Fn тогда и только тогда, когда ((F1ÙF2Ù...ÙFn) G)общезначима.
G)общезначима.
Теорема 2. Пусть даны формулы F1,F2,...,Fn и формула G. Тогда G есть логическое следствие F1,F2,...,Fn тогда и только тогда, когда (F1ÙF2Ù...ÙFnÙØG) противоречива.
Теоремы 1 и 2 очень важны. Из них вытекает: доказательство того, что отдельная формула есть логическое следствие конечного множества формул, эквивалентное доказательству того, что некоторая связанная с ними формула общезначима или противоречива. Если G есть логическое следствие формул F1,F2,...,Fn , то формула ((F1ÙF2Ù...ÙFn) G) называется теоремой, а G называется также заключением теоремы. В математике, так же, как и в других областях, многие проблемы могут быть сформулированы как проблемы доказательства теорем.
G) называется теоремой, а G называется также заключением теоремы. В математике, так же, как и в других областях, многие проблемы могут быть сформулированы как проблемы доказательства теорем.
Рассмотрим примеры решения типичных упражнений и задач
1. Даны формулы логики высказываний: F1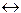 (P
(P Q), F2
Q), F2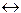 ØQ, G
ØQ, G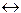 ØP.
ØP.
Показать, что G есть логическое следствие F1 и F2.
Решение. Метод 1. Используем метод истинностных таблиц, чтобы показать, что G истинна в каждой модели формулы (P Q)ÙØQ. (Когда интерпретация I удовлетворяет формуле F, I называется моделью F). Из табл.3.4 мы видим, что есть только одна модель для (P
Q)ÙØQ. (Когда интерпретация I удовлетворяет формуле F, I называется моделью F). Из табл.3.4 мы видим, что есть только одна модель для (P Q)ÙØQ, а именно {ØP, ØQ}.
Q)ÙØQ, а именно {ØP, ØQ}.
Таблица9.4 - Истинностная таблица (P Q)ÙØQ и ØP.
Q)ÙØQ и ØP.
| P Q | P Q Q
| ØQ | (P Q)ÙØQ Q)ÙØQ
| ØP |
| 0 0 0 1 1 0 1 1 |
Формула ØP истинна в этой модели. Таким образом, по определению логического следствия заключаем, что ØР есть логическое следствие (P Q) и ØQ.
Q) и ØQ.
Метод 2. Используем теорему 1. Это может быть сделано просто путем расширения истинностной таблицы в табл.9.4, т.е. путем вычисления истинностных значений формулы ((P Q)ÙØQ)
Q)ÙØQ) ØP. Табл.3.5 показывает, что ((P
ØP. Табл.3.5 показывает, что ((P Q)ÙØQ)
Q)ÙØQ) ØP истинна при всех интерпретациях.
ØP истинна при всех интерпретациях.
Таблица 9.5 - Истинностная таблица для ((P Q)ÙØQ)
Q)ÙØQ) ØP
ØP
| P Q | P Q Q
| ØQ | (P Q)ÙØQ) Q)ÙØQ)
| ØP | ((P Q)ÙØQ) Q)ÙØQ) ØP ØP
|
| 0 0 0 1 1 0 1 1 |
Следовательно, ((P Q)ÙØQ)
Q)ÙØQ) ØP общезначима и, согласно теореме 1, ØP есть логическое следствие (P
ØP общезначима и, согласно теореме 1, ØP есть логическое следствие (P Q) и ØQ.
Q) и ØQ.
Мы можем также доказать общезначимость формулы путем преобразования ее в конъюнктивную нормальную форму:
((P Q)ÙØQ)
Q)ÙØQ) ØP=Ø((P
ØP=Ø((P Q)ÙØQ)ÚØP=
Q)ÙØQ)ÚØP=
=Ø((ØPÚQ)ÙØQ)ÚØP=Ø((ØPÙØQ)Ú(QÙØQ))ÚØP=
=Ø((ØPÙØQ)ÚЛ)ÚØP=Ø(ØPÙØQ)ÚØP=(PÚQ)ÚØP=
=QÚ (PÚØP)=QÚU=U.
Таким образом, ((P Q)ÙØQ)
Q)ÙØQ) ØP общезначима.
ØP общезначима.
Метод 3. Используем теорему 2. В этом случае мы докажем, что формула ((P Q)ÙØQ)Ù(Ø(ØP))=(P
Q)ÙØQ)Ù(Ø(ØP))=(P Q)ÙØQÙP противоречива. Как и в методе 2, можно использовать метод истинностных таблиц, чтобы показать, что (P
Q)ÙØQÙP противоречива. Как и в методе 2, можно использовать метод истинностных таблиц, чтобы показать, что (P Q)ÙØQÙP ложна в каждой интерпретации. Из табл.11.6 мы заключаем, что (P
Q)ÙØQÙP ложна в каждой интерпретации. Из табл.11.6 мы заключаем, что (P Q)ÙØQÙP противоречива и, согласно теореме 2, ØP есть логическое следствие формул (P
Q)ÙØQÙP противоречива и, согласно теореме 2, ØP есть логическое следствие формул (P Q) и ØQ.
Q) и ØQ.
Таблица 9.6 - Истинностная таблица для (P Q)ÙØQÙP
Q)ÙØQÙP
| P Q | P Q Q
| ØQ | (P Q)ÙØQÙP Q)ÙØQÙP
|
| 0 0 0 1 1 0 1 1 |
Мы можем также доказать противоречивость формулы (P Q)ÙØQÙP путем ее преобразования в дизъюнктивную нормальную форму:
Q)ÙØQÙP путем ее преобразования в дизъюнктивную нормальную форму:
(P Q)ÙØQÙP=(ØPÚQ)ÙØQÙP=(ØPÙØQÙP)Ú(QÙØQÙP)=
Q)ÙØQÙP=(ØPÚQ)ÙØQÙP=(ØPÙØQÙP)Ú(QÙØQÙP)=
=(ЛÙØQ)Ú(ЛÙP)=ЛÚЛ=Л. Таким образом, (P Q)ÙØQÙP противоречива.
Q)ÙØQÙP противоречива.
2. Покажем применение логики высказываний при решении задач в словесной формулировке. Допустим, что если конгресс отказывается принять новые законы, то забастовка не будет окончена, если только она не длится более года и президент фирмы не уходит в отставку. Закончится ли забастовка, если конгрес отказывается действовать и забастовка только что началась?
Решение. Сперва преобразуем утверждения в символы:
Р: Конгресс отказывается действовать.
Q: Забастовка оканчивается.
R: Президент фирмы уходит в отставку.
S: Забастовка длится более года.
Тогда факты, данные в примере, могут быть представлены следующими формулами:
F1: (P (ØQÚ(RÙS)))
(ØQÚ(RÙS))) 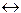 Если конгресс отказывается принять новые законы, то забастовка не будет окончена, если она не длится более года и президент фирмы не уходит в отставку.
Если конгресс отказывается принять новые законы, то забастовка не будет окончена, если она не длится более года и президент фирмы не уходит в отставку.
F2: P 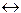 Конгресс отказывается действовать.
Конгресс отказывается действовать.
F3: ØS 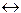 Забастовка только что началась.
Забастовка только что началась.
Можно ли заключить из фактов F1, F2 и F3, что забастовка не будет окончена, т.е. можно ли показать, что ØQ есть логическое следствие F1, F2 и F3? По теореме 1 это эквивалентно тому, что ((P (ØQÚ(RÙS)))ÙPÙØS)
(ØQÚ(RÙS)))ÙPÙØS) ØQ ¾ общезначимая формула. Истинностные значения указанной формулы при всех интерпретациях приведены в табл. 9.7.
ØQ ¾ общезначимая формула. Истинностные значения указанной формулы при всех интерпретациях приведены в табл. 9.7.
Таблица 9.7 - Истинностная таблица для (F1 Ù F2 Ù F3) ØQ,
ØQ,
где F1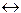 (P
(P (ØQÚ(RÙS))), F2
(ØQÚ(RÙS))), F2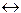 Р, F3
Р, F3 ØS
ØS
| P | Q | R | S | F1 | F2 | F3 | ØQ | (F1ÙF2ÙF3) ØQ ØQ
|
Из табл 9.7 видно, что не существует интерпретации, при которой данная формула ложна. Следовательно, формула ((P (ØQÚ(RÙS)))ÙPÙØS)
(ØQÚ(RÙS)))ÙPÙØS) ØQ общезначима. Поэтому ØQ есть логическое следствие F1,F2 и F3, т.е. мы можем получить заключение ØQ из F1,F2 и F3. Следовательно, забастовка не будет окончена.
ØQ общезначима. Поэтому ØQ есть логическое следствие F1,F2 и F3, т.е. мы можем получить заключение ØQ из F1,F2 и F3. Следовательно, забастовка не будет окончена.
Из приведенных примеров видно, что логика высказываний может применяться ко многим задачам. Метод состоит в том, чтобы сначала записать задачи формулами, а затем доказать, что формулы общезначимы или противоречивы. Процедуру доказательства противоречивости формулы путем ее преобразования в ДНФ и получение противоречивой формулы (Л) иногда называют методом умножения, потому что процесс преобразования очень похож на раскрытие скобок в произведении сумм.
Мы показали использование метода истинностных таблиц и метода умножения для доказательства общезначимости (или противоречивости).
Контрольные вопросы и задания по теме:
1. Логическое следствие в ЛВ.
2. Теоремы 1 и 2 об установлении логического следствия.
3. Методы установления истинности или противоречивости формул ЛВ.
4. Докажите, что (ØQ ØP) есть логическое следствие(P
ØP) есть логическое следствие(P Q).
Q).
5. Если конгресс отказывается принять новые законы, то забастовка не будет окончена, кроме случая, когда она длится более года и президент фирмы уйдет в отставку. Допустим, что конгресс отказывается действовать, забастовка оканчивается и президент фирмы не уходит. Длилась ли забастовка более года?
6. Даны утверждения
F1: P S,
S,
F2: S U,
U,
F3: P,
G: U.
Является ли G логическим следствием F1,F2 и F3?
7. Покажите, что Q есть логическое следствие (P Q) и P. Это так называемое правило модус поненс (modus ponens).
Q) и P. Это так называемое правило модус поненс (modus ponens).
# Формализация высказываний средствами логики первого порядка.