Второй закон Ньютона.
Массой тела называют физическую величину, являющуюся мерой его инерционных свойств.
Свойство тела сохранять свое состояние неизменным называют инерцией, а системы отсчета, в которых выполняется этот закон, - инерциальными.
Определение 2.
Причина изменения состояния тела, т.е. появление ускорения связана с введением понятия силы.
Определение 3.
Силой называют количественную меру простого воздействия на тело со стороны других тел, во время действия которого тело или его части получают ускорения.
В международной системе единиц СИ силу измеряют в Ньютонах ( Н ).
Однако существуют метрические внесистемные единицы: грамм, килограмм и тонна. Эти единицы используются при определении веса тела.
На практике для измерения величины силы используют динамометр - тарированную (градуированную) пружину, снабженную шкалой.
Второй закон Ньютона – дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта.
 Формулировка:
Формулировка:
Ускорение, приобретаемое материальной точкой в инерциальной системе отсчета:
- прямо пропорционально действующей на точку (равнодействующей) силе;
- обратно пропорционально массе точки; и
- направлено в сторону действия силы.
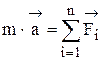 , (1)
, (1)
Ускорение – вектор, масса – величина скалярная (число), поэтому сила тоже есть вектор, направление которого совпадает с направлением ускорения. Уравнение (1) представляет одну из форм записи второго закона Ньютона.
В механике это уравнение принято называть уравнением движения.
В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:
Определение 1.
Импульсом называется величина , где
, где  скорость тела.
скорость тела.
В ньютоновской механике предполагается, что масса тела постоянна и не зависит от скорости, поэтому левую часть уравнения (1) можно переписать в виде:
 . ( 2 )
. ( 2 )
С учетом ( 2 ) уравнение ( 1 ) принимает вид:
 . ( 3 )
. ( 3 )
Интерпретация: