Внутренняя энергия, первое начало термодинамики

Равновесные процессы в идеальном газе.

Теплоемкость идеального газа.

4. Виды равновесных процессов.

Определение 1.

Внутренней энергией объектаназывают часть его полной энергии за вычетом кинетической энергии движения объекта, как целого, и его потенциальной энергии во внешнем поле.

 

Таким образом, во внутреннюю энергию входят кинетическая энергия поступательного и вращательного движений молекул, потенциальная энергия их взаимодействия, энергия колебательного движения атомов в молекулах, а также энергия различных видов движения частиц в атомах.

Внутренняя энергия системы может изменяться за счет энергии, сообщаемой системе извне. Эта энергия может сообщаться системе посредством двух процессов: либо за счет работы, производимой внешними силами над системой, либо за счет передачи ей тепла.

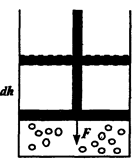
Рассмотрим газ, сжимаемый в сосуде поршнем под действием силы FПусть под действием этой силы поршень переместился на расстояние dh, сжав газ. Работа силы на пути dh –это dA = Fdh.

Разделив величину силы на площадь поршня, получим давлениеP, а умножив на S, получим изменение объема газа dV.

Таким образом, производимая над газом работа будет равна dA= P·dV.

Такую же по величине работу совершает газ при расширении, перемещая поршень. При этом dVположительно, если газ расширяется, и отрицательно при сжатии газа.

Соответственно работа dAположительна или отрицательна:

· в первом случае система производит работу сама,

· во втором — внешние силы производят работу над системой.

 

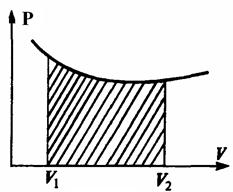
Графически процесс изменения состояния газа при его расширении или сжатии изображается на кривой P (V)участком на графике.

Полная работа, совершаемая газом, при расширении от V₁до V₂:.

Эта работа численно равна заштрихованной площади, заключенной под кривой P (V).

Передачу теплоты, как энергии, передаваемой от одного тела другому, описывает закон, названный первым началом термодинамики:

 

dQ = dE + dA = dE + P·dV, (1)

 

гдеQ –теплота, E –внутренняя энергии системы, A –произведенная работа.

 

Это уравнение представляет собой закон сохранения энергии применительно к механической и тепловой энергии макроскопических тел.