Расчет осевых моментов инерции твердых тел

Уравнение (5.12) называют основным уравнением динамики вращения. Из него следует, что угловое ускорение e твердого тела, вращающегося вокруг неподвижной оси, прямо пропорционально результирующему моменту относительно этой оси всех внешних сил, действующих на тело, и обратно пропорционально моменту инерции тела относительно той же оси.

Таким образом, момент инерции тела является мерой его инертности при вращательном движении вокруг неподвижной оси: при одном и том же значении момента сил M_zтело с большим моментом инерции приобретает меньшее угловое ускорение ε.

Для определения момента инерции твердого тела относительно оси его разбивают на элементарные массы 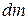и сумму в выражении (4.11) заменяют интегралом:

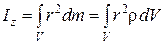, (5.14)

где ρ – плотность тела. Интегрирование выполняется по всему объему тела.

При вычислении осевого момента инерции твердого тела используются следующие его основные свойства.

1. Аддитивность. Момент инерции тела равен алгебраической сумме моментов инерции отдельных его частей.

2. Теорема Штейнера. Эта теорема применяется для расчета моментов инерции тел, если ось вращения не проходит через центр инерции тела (его центр масс): момент инерции I тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр массы С данного тела и параллельной заданной оси, и произведения массы m тела на квадрат расстояния между этими осями (рис. 5.4)

I = I_C + md². (5.15)

Рис.5.4

Пример 4.2 Момент инерции тонкого стержня. Длина стержня l, масса m. Найти момент инерции относительно оси, проходящей перпендикулярно стержню через его центр (рис. 4.7) и через один из его концов.

Сначала найдем момент инерции относительно оси, проходящей через центр стержня. Выделим элемент длины стержня длиной dx на расстоянии x оси вращения. Тогда масса этого элемента равна 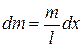, а момент инерции 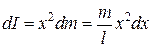. Момент инерции определим по формуле (4.15), интегрируя по переменной x в пределах от до :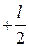

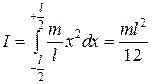Рис. 4.7

Момент инерции относительно оси, проходящей через один из его концов, найдем с помощью теоремы Штейнера (4.16):

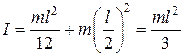В таблице 1 приведены формулы для вычисления моментов инерции однородных тел простейшей формы.

Таблица 1

Тело	Положение оси	Момент инерции
1. Полый тонкостенный цилиндр радиуса R и массой m	Ось симметрии	I_z = mR²
2. Сплошной цилиндр (или диск) радиуса R и массой m	Ось симметрии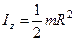
3. Прямой тонкий стержень длиной l и массой m	Ось перпендикулярна стержню и проходит через его конец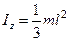
4. Тот же стержень	Ось перпендикулярна стержню и проходит через его середину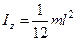
5. Шар радиуса R и массой m	Ось проходит через центр шара