Закон изменения и сохранения момента импульса

ДИНАМИКА ТВЕРДОГО ТЕЛА

ЛЕКЦИЯ 5

Твердое тело можно рассматривать как систему материальных точек, жестко связанных друг с другом. Оказывается, что количество уравнений для описания отдельных видов движений можно значительно уменьшить, если ввести физические величины, которые относятся ко всему твердому телу.

Рассмотрим произвольную систему частиц (материальных точек), которая перемещается относительно некоторой неподвижной точки О (рис. 4.1). Для каждой точки данной системы запишем второй закон Ньютона

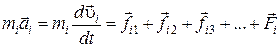, (5.1)

где 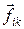(k = 1, 2, …, n) представляют собой внутренние силы взаимодействия всех элементов тела с выбранным элементом i, а 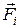– равнодействующая всех внешних сил, действующих на этот элемент, m_i – масса i-го элемента.

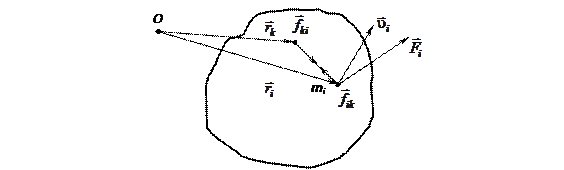
Рис. 5.1

Умножим векторно слева уравнение (5.13) на радиус - вектор точки i-го элемента, :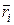

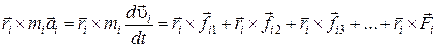. (5.2)

Преобразуем левую часть:

(5.3)

Величина 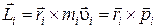в (5.3) называется моментом импульса материальной точки (векторное произведение радиус – вектора точки на ее импульс).

Величину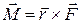, равную векторному произведению радиус-вектора точки на вектор силы, действующей на точку A, на­зывают моментом силы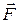относительно точки О(рис. 4.5). Таким образом, величина 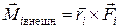в правой части (5.15) есть момент внешней силы, действующей на точку i. Величина в уравнении (5.2), равная:

,

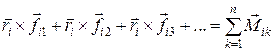есть сумма моментов всех внутренних сил, действующих на точку i. С учетом введенных обозначений уравнение (5.2) примет вид:α

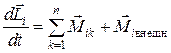. (5.4)

Просуммируем уравнения движения по всем n элементам системы:

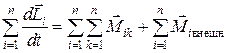. (5.5)

Левая часть (5.5) представляет собой момент импульса системы, который равен векторной сумме моментов составляющих систему точек:

. (5.6)

Первое слагаемое в (5.5) есть сумма моментов всех внутренних сил, действующих на систему. Можно показать, что эта сумма равна нулю. В самом деле, рассмотрим сумму моментов внутренних сил для двух точек, i и k (рис. 5.1). Учитывая, что по 3-му закону динамики 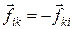, получим:

,

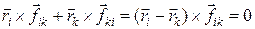так как вектор, равный разности 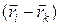, направлен вдоль сил 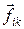и . Если попарно просуммировать моменты внутренних сил, то получим, что сумма моментов всех внутренних равна нулю.

Уравнение (5.5) для тела из материальных точек можно представить в виде:

. (5.7)

Таким образом, скорость изменения момента импульса системы относительно неподвижной точки равна результирующему моменту относительно той же точки всех внешних сил, действующих на систему. Согласно урав­нению (5.7) момент импульса системы может изменять­ся под действием только суммарного момента всех внеш­них сил.

Если внешние силы отсутствуют, т.е. 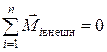, то система замкнута и из (4.7) следует закон сохранения момента им­пульса механической системы: момент импульса замкнутой системы частиц остается по­стоянным.

Моменты импульса отдельных частей или час­тиц замкнутой системы могут изменяться со временем, однако эти изменения всегда происходят так, что приращение мо­мента импульса одной части системы равно убыли мо­мента импульса ее другой части (относительно одной и той же точки системы отсчета).

Момент импульса 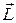сохраняется для незамкнутых систем, у ко­торых, импульс 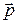меняется со временем. Если относительно некоторой точки О выбранной систе­мы отсчета суммарный момент внешних сил 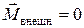, то, со­гласно (5.7), момент импульса системы относительно точки О сохраняется.

В частном случае у незамкнутых систем может сохраняться не сам момент импульса 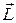, а его проекция на некоторую неподвижную ось z, когда проекция суммарного момента всех внешних сил на эту ось равна нулю. За­писав уравнение (5.7) в проекциях на ось z, получим:

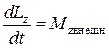. (5.8)

Здесь L_iz и М_{iz внешн} - момент импульса и суммарный мо­мент внешних сил относительно оси z для i-й частицы системы:

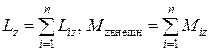. (5.9)

Из уравнения (5.8) следует, что если проекция М_zвнешн =0, то момент импульса системы относи­тельно этой оси сохраняется:

.

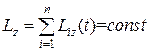Момент силы относительно оси z в (5.8) можно определить, раскрыв векторное произведение по формуле:

М_zвнешн=rF_внешнsinα=F_внешнl, (5.10)

где величина l =rsinα называется плечом силы (кратчайшее расстояние от оси до направления действия силы, см. рис.5.2).

 

 

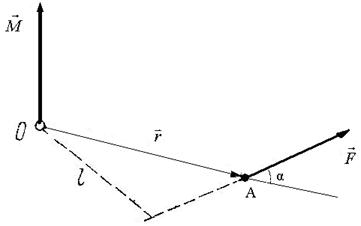
Рис.5.2

Пример 5-1. Расчет момента сил трения.

Диск, радиус которого R и масса m вращается на плоской поверхности вокруг неподвижной оси (рис.4.3). Коэффициент трения скольжения материала диска равен m. Найти момент сил трения диска о поверхность

Момент сил трения, действующих на весь диск, алгебраически складывается из моментов сил трения, действующих на элементарные участки диска массой dm, и направлен перпендикулярно его плоскости (рис.5.3).

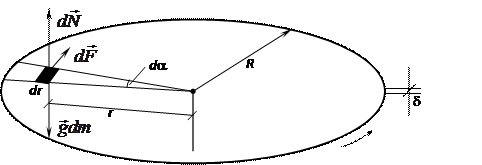Рис. 5.3

Выделим элемент объема dV = drdrda диска на расстоянии r от центра (d – толщина диска). Сила трения скольжения, приложенная к этому элементу равна dF = mgdm. Момент силы трения скольжения для элемента, находящегося на расстоянии r от оси вращения равен:

dM = dF · r = mgrdm,

где dm = rdV = rdrdrda – масса элемента объема диска. Тогда суммарный момент сил трения получим, интегрируя выражение для dM по r в пределах от 0 до R и по a в пределах от 0 до 2π:

.

При получении последнего выражения учитывалось, что масса диска равна m = rdpR².

. Наряду с за­конами сохранения энергии и импульса закон сохранения момента импульса является одним из фундаментальных законов природы.