Свойства равносильности уравнений и неравенств

Задание

Лекция № 8-9. Уравнения, неравенства и их системы в ШКМ

Цели лекции:

1) раскрыть базовые вопросы темы «Уравнения, неравенства и их системы» ШКМ: понятие уравнения (неравенства), системы уравнений (системы неравенств), совокупности уравнений (неравенств); определение корня уравнения (решения неравенства), решения системы уравнений (системы неравенств), решения совокупности уравнений (совокупности неравенств); понятие равносильности уравнений (неравенств) и их свойства; виды уравнений (неравенств) ШКМ и способы их решения; методы решения систем уравнений;

2) раскрыть базовые способы соблюдения равносильности уравнений и неравенств: применять только свойства равносильности; сохранять область определения и множество значений двух частей уравнения (неравенства);

3) выделить элементы математической культуры как компетенции: прием доказательства совпадения двух множеств; прием изложения идеи доказательства на конкретном примере; взаимосвязь понятий равносильность и следствие; способы сведения сложных уравнений к линейным и/или квадратным уравнениям;

4) раскрыть способы организации записей лекции как компетенции: обозначение подразделов в заголовке раздела; составление заголовков к разделам текста; использование двухэтажных записей для обозначения взаимосвязанных утверждений; использование таблицы не только для систематизации информации, но и для перевода фактов с одного языка на другой.

По формулировкам целей лекции сформулируйте вопросы, на которые предстоит ответить в лекции.

___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

 

 

План.

I. Основные понятия.

II. Виды уравнений (неравенств) и способы их решения.

III. Уравнения и неравенства с модулем.

IV. Методы решения систем уравнений.

I. Основные понятия (основные определения; равносильность У и Н).

Основные определения

Определение. Уравнением с одной переменной называется математическая запись, содержащая знак равенства и одну переменную, если ставится задача найти все значения переменной, при которых равенство становится верным числовым равенством.

Значение переменной, при которой уравнение обращается в верное числовое равенство, называется ________________________.

Определение. Неравенством с одной переменной называется _________________ ___________, содержащая знак _____________ и одну переменную, если ставится задача найти все значения переменной, при которых неравенство становится верным числовым неравенством.

Значение переменной, при которой неравенство обращается в верное числовое неравенство, называется _________________________.

Определение. Системой уравнений с двумя переменными называется набор уравнений, если ставится задача найти все пары значений переменных, при которых каждое уравнение становится верным числовым равенством.

Для обозначения системы уравнений используется знак:.

Пара значений переменных, при которых каждое уравнение становится верным числовым равенством, называется решением системы уравнений.

Множество всех решений системы уравнений является _________________________ решений каждого из них.

Определение. Совокупностью уравнений с двумя переменными называется набор уравнений, если ставится задача найти все пары значений переменных, при которых хотя бы одно уравнение становится верным числовым равенством.

Для обозначения системы уравнений используется знак:.

Пара значений переменных, при которых хотя бы одно уравнение становится верным числовым равенством, называется решением совокупности уравнений.

Множество всех решений совокупности уравнений является _____________________ решений каждого из них.

Пример.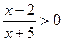

Дробь больше 0, если числитель и знаменатель одного знака. Возможны два случая: числитель и знаменатель положительны или числитель и знаменатель отрицательны.

Союз «и» говорит о том, что мы имеем дело с системой неравенств, союз «или» – с совокупностью.

 

Ответ: (–¥; –5) È (2; +¥ )

Равносильность уравнений

Определение. Два уравнения называются равносильными, если множества их решений совпадают, т.е. каждый корень первого уравнения является корнем второго уравнения, и каждый корень второго уравнения является корнем первого уравнения.

Если два уравнения не имеют корней, то они считаются равносильными.

Аналогично определяется равносильность неравенств, систем и совокупностей.

№	Свойства равносильности уравнений	Свойства равносильности неравенств
1.	Если к обеим частям
уравнения	неравенства
прибавить одно и то же число, то получится
уравнение,	неравенство,
равносильное данному.
2.	Если обе части
уравнения	неравенства
умножить на число,
отличное от нуля,	большее 0,	меньшее 0, и при этом поменять знак неравенства на противоположный,
то получится
уравнение,	неравенство,
равносильное данному.
3.	Если в какой-то части
уравнения	неравенства
выполнить тождественное преобразование, то получится
уравнение,	неравенство,
равносильное данному.