III. Уравнения и неравенства с модулем.

Элемент математической культуры как компетенция

ЭМК О способах сведения сложных уравнений к простейшим

1. Применение равносильных преобразований (пример: сведения к линейному уравнению).

2. Замена уравнения совокупностью (произведение равно 0, если хотя бы 1 множитель равен 0, а другой при этом не теряет смысла). Чтобы применить этот способ, нужно предварительно все слагаемые перенести в левую часть и разложить ее на множители.

3. Замена уравнения системой уравнения и неравенства (пример: дробно-рациональные уравнения).

4. Метод замены переменных (пример: биквадратные уравнения).

Основная идея: раскрыть модуль. Для этого надо знать, какой знак принимает подмодульное выражение.

Схема решения.

1. Найти модульные нули.

2. Нанести найденные нули на координатную прямую и выделить образовавшиеся интервалы.

3. Определить знак каждого подмодульного выражения на каждом из интервалов.

4. Решить уравнение (неравенство) на каждом из интервалов: 1) раскрыть модуль на выбранном интервале; 2) решить полученное уравнение (неравенство); 3) выбрать решения, попадающие в выбранный интервал.

Пример 1. Решить неравенство: ïх² – 5х + 4ï> х –3.

Шаг 1. Найдем модульные нули.

____________ = 0; х = ___, х = ___.

Шаг 2. Нанесем найденные нули на координатную прямую и выделим образовавшиеся интервалы.

 

 

Шаг 3. Определим знак каждого подмодульного выражения на каждом из интервалов.

 

Шаг 4. Решим неравенство на каждом из интервалов:

а) х £ __ б) __£ х £ __ в) х ³ __

1) раскрываем модуль

_____________ > х – 3;

2) решаем полученное неравенство

х² – 6х + 7 > 0

х² – 6х + 7 = 0

х = 3 –….., х = 3 + …

 

 

3) выберем решение, попадающее в интервал

 

х Î ________.

Самостоятельно рассмотреть остальные случаи.

 

Ответ: _________________________________________________________________

Пример 2. Решить неравенство: ïх² – 5х + 4ï> ïх –3ï.

Что изменится? (добавится еще один модульный нуль: число _____; появятся новые интервалы; на каждом из интервалов надо учитывать знак двух подмодульных выражений). Совет: Знаки на интервалах располагать в порядке следования модулей в заданном неравенстве.

 

 

Самостоятельно решить.

Пример 3. Решить уравнение: ïх² – 5х + 4ï= ïх –3ï.

Что изменится?

а) х £ 1

1) раскрываем модули

х² – 5х + 4 = –х + 3;

2) решаем полученное уравнение

х² – 4х + 1 = 0

х = 2 – 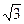; х = 2 +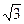

3) выберем решение, попадающее в интервал

 

 

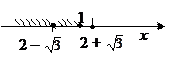х = 2 – .

Самостоятельно рассмотреть остальные случаи.

Замечание.

1. Если дано уравнение или неравенство вида ïf(х)ï Ú а, то надо уметь устно избавляться от модуля.

2. Если дано уравнение или неравенство вида ах² + bïхï + с Ú 0, то удобно решать заменой переменных: ïхï = t.