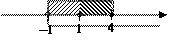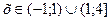Лекция № 8-9. Уравнения, неравенства и их системы в ШКМ (часть 2).
II. Виды уравнений (неравенств) и способы их решения.
- Уравнения и неравенства 1-ой степени.
Самостоятельно: Решите уравнение (неравенство) 1-ой степени, выделяя шаги решения.
| Уравнение 2(3 – 4х) + 5 = х – 3 | Неравенство 2(3 – 4х) + 5 < х – 3 |
| 1. Раскрыть скобки | |
| 2. Перенести слагаемые, содержащие неизвестную, в одну часть уравнения (неравенства), поменяв при этом знак переносимого слагаемого на противоположный | |
| Привести подобные слагаемые | |
| 4. Обе части уравнения (неравенства) разделить на коэффициент при неизвестной (если он не равен 0). При решении неравенств, если коэффициент отрицательный, то знак неравенства сменить на противоположный. | |
| 5. Записать ответ | 5. Нанести решение на числовую прямую |
| 6. Записать ответ в виде промежутка | |
- Уравнения и неравенства 2-ой степени.
Самостоятельно: Решите уравнения (неравенства) 2-ой степени, выделяя шаги решения.
Уравнение 1: х2 – 6х + 8 = 0.
| Способ 1 (через дискриминант) | Способ 2 (по формуле четного коэффициента) | Способ 3 (по теореме, обратной теореме Виета, если а = 1) |
| 1. Найти дискриминант D = | 1. Найти ¼ дискриминанта по формуле: 
| 1. Составить систему:
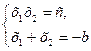
|
2. Вычислить корни по формуле х1, 2 = 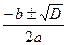 , если D ³ 0. , если D ³ 0.
| 2. Вычислить корни по формуле х1, 2 =  , если D ³ 0. , если D ³ 0.
| 2. Перечислить модули чисел так, чтобы их произведение равнялось 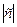
|
| 3. Определить знаки корней (если произведение положительно, то корни имеют тот же знак, что и сумма корней; если произведение отрицательно, то корни имею разный знак). Корни данного уравнения ……………………………… | ||
4. Подобрать корни по заданной сумме: =… =… 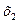 = =
|
Уравнение 2: х2 + 2х – 8 = 0
| Способ 1 (через дискриминант) | Способ 2 (по формуле четного коэффициента) | Способ 3 (по теореме, обратной теореме Виета, если а = 1) |
х2 – 6х + 8 > 0.
| Способ 1 (метод интервалов) | Способ 2 (схематическое построение параболы) | |||
1. Найти нули (составить уравнение и найти его корни)
 =… =… 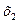 = … = …
| 1. Определить точки пересечения параболы с осью Ох (решить квадратное уравнение)
 =… =… 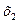 = … = …
| |||
2. Построить интервалы (нанести нули на числовую прямую и выделить интервалы)

| 2. Определить направление ветвей параболы (если а > 0, то ветви – вверх, если а < 0, то ветви – вниз). а = … …0, значит, ветви направлены… | |||
3. Определить знак выражения (функции) на каждом из интервалов (для квадратичной функции знаки чередуются, значит, достаточно определить знак на одном из интервалов).
|    3. Построить схематически график 3. Построить схематически график
| |||
4. Выбрать промежутки, соответствующие неравенству
| 4. Отметить промежутки, соответствующие неравенству, и записать ответ:
|
Самостоятельно: Запишите ответ для следующих неравенств:
| Неравенство | х2 – 6х + 8 < 0. | х2 – 6х + 8 ³ 0. |
| Ответ |
- Дробно-рациональные уравнения и неравенства.
Уравнение 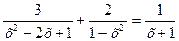
| Неравенство: 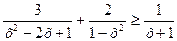
| |||||||
1. Свести уравнение к виду: «дробь» = 0
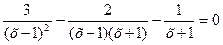
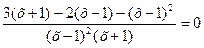
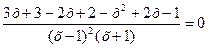
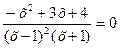
| 1. Свести неравенство к виду: «дробь» «знак неравенства» 0
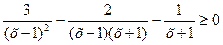
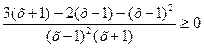

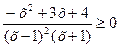
| |||||||
2. Составить систему («дробь» = 0, когда «числитель» = 0, а «знаменатель» ¹ 0).
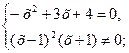
| 2. Составить две системы, при которых дробь будет иметь заданный знак
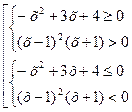
| 2. Решить неравенство методом интервалов (НИЗО)
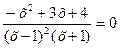
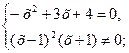
| ||||||
3. Решить систему (решить 1-ое уравнение; сделать проверку, удовлетворяют ли корни условию «знаменатель» ¹ 0).
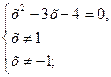
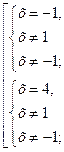 Þ х = 4
Ответ: 4. Þ х = 4
Ответ: 4.
| 3. Решить составленные системы неравенств.
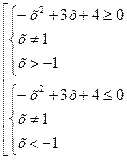

 ; х = –1; х = 4. ; х = –1; х = 4.
Ответ: | 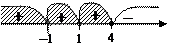 

|
Замечание. Неравенство 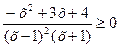 можно было упростить.
можно было упростить.
Способ 1. Умножить обе части неравенства на –1:
 .
.
Способ 2. Разложить числитель на множители и сократить дробь:
 ;
; 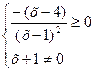 ;
;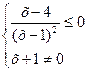 ;
; ;
;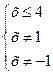 ;
;