Лекция № 4. Дискретные и непрерывные случайные величины

При проведении стохастического эксперимента формируется пространство элементарных событий – возможных исходов этого эксперимента. Считают, что на этом пространстве элементарных событий задана случайная величина X, если задан закон (правило) по которому каждому элементарному событию сопоставляется число. Таким образом, случайную величину X можно рассматривать, как функцию, заданную на пространстве элементарных событий.

■ Случайная величина - величина, которая при каж­дом испытании прини­мает то или иное числовое значение (на­перед неизвестно, какое именно), зависящее от случайных при­чин, которые заранее не могут быть учтены. Случайные величины обозначают за­главными буквами латинского алфавита, а возможные значе­ния случайной величины – малыми. Так, при бросании игрального кубика проис­ходит событие, связанное с числом x , где x – выпавшее число очков. Число очков – случайная величина, а числа 1, 2, 3, 4, 5, 6 – возможные значе­ния этой величины. Расстояние, которое пролетит снаряд при выстреле из орудия – тоже случайная величина (зависит от установки при­цела, силы и направления ветра, температуры и других факто­ров), а возможные значения этой величины принадлежат неко­торому промежутку (a; b).

■ Дискретная случайная величина – случайная величина, которая принимает отдельные, изо­лированные возмож­ные значения с определенными вероятно­стями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным.

■ Непрерывная случайная величина – случайная величина, которая может принимать все значения из некоторого конечного или бесконечного проме­жутка. Число возможных значений непрерывной случайной величины – беско­нечно.

Например, число выпавших очков при бросании кубика, балльная оценка за кон­трольную работу – дискретные случайные величины; рас­стояние, которое пролетает снаряд при стрельбе из орудия, по­грешность измерений показателя времени усвоения учебного мате­риала, рост и вес человека – непрерывные случайные величины.

■ Закон распределения случайной величины – соответствие между возмож­ными значениями случайной величины и их вероятностями, т.е. каждому воз­можному значению x_i ставится в соответствие ве­роятность p_i, с которой случайная величина может принять это значение. Закон распределения случайной величины может быть задан таблично (в форме таблицы), аналитиче­ски (в виде формулы) и графически.

Пусть дискретная случайная величина X принимает значения x₁, x₂, …, x_n с ве­роятностями p₁, p₂, …, p_n соответственно, т.е. P(X=x₁) = p₁, P(X=x₂) = p₂, …, P(X=x_n) = p_n. При табличном задании закона распределения этой величины первая строка таблицы содержит воз­можные значения x₁, x₂, …, x_n, а вторая – их вероятности (см. рис. 2.3).

 

X	x1	x2	…	xn
p	p1	p2	…	pn

 

Рис. 2.3

В результате испытания дискретная случайная величина X принимает одно и только одно из воз­можных значений, поэтому события X=x₁, X=x₂, …, X=x_n образуют полную группу попарно несовместных событий, и, значит, сумма вероятностей этих событий равна единице, т.е. p₁ + p₂ +… + p_n =1.

Пример 2.23. Студент сдает два экзамена: по математике и инфор­матике. Составьте закон распре­деления случайной величины X, числа полученных пятерок, если вероятность получения пятерки по матема­тике равна 0,7, а по информатике – 0,6.

Решение. Пусть A₁ и A₂ – события, заключающиеся в том, что ма­тематика и информатика сданы на «5». Возможные значения X есть 0, 1, 2, причем

P(X=0) = P(`A<sub>1</sub> ·`A₂) = P(`A<sub>1</sub>) · P(`A₂) = (1-0,7)·(1-0,6) = 0,3·0,4 = 0,12;

P(X=1) = P(A₁·`A<sub>2</sub> +`A₁ ·`A<sub>2</sub>) = P(A<sub>1</sub>·`A₂) + P(`A₁ · A₂) = 0,7·0,4 + 0,3·0,6 = 0,46;

P(X=2) = P(A₁ ·A₂) = P(A₁) · P(A₂) = 0,7·0,6 = 0,42.

Следовательно, закон распределения данной случайной величины в форме таблицы и в виде гра­фика будет таким (см. рис. 2.4).

Контроль: 0,12 + 0,46 + 0,42 = 1.

 

 

а) б)

Рис. 2.4

■ Функция распределения случайной величины – функция F(x), определяющая для каждого значе­ния x вероятность того, что случайная вели­чина X примет значение, меньшее x, т.е.

F(x) = P(X<x).

Эта функция используется для задания распределений как дискретных, так и не­прерывных С.в.

При известном законе распределения Ф.р. дискретной слу­чайной величины имеет вид F(x) = P(X<x) =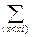p_i, где (x<x_i) озна­чает, что суммирование ведется по всем ин­дексам i, для ко­торых это неравенство выполнимо.

▲Теорема 2.16. Функция F(x) – неубывающая функция, т.е. F(x₂) ³ F(x₁), если x₂ ³x₁.

Следствие 1. Вероятность того, что случайная величина примет значение из ин­тервала (a; b), равна приращению функции распределения на этом интервале, т.е. P(a£X<b) = F(b) – F(a).

Следствие 2. Вероятность того, что непрерывная слу­чайная величина X примет одно определенное значение, равна нулю.

▲Теорема 2.17. Если возможные значения случайной ве­личины принадлежат ин­тервалу (a; b), то: 1) F(x) = 0 при x£a; 2) F(x) = 1 при x³b.

Доказательство этой теоремы опускается.

Следствие. Если возможные значения непрерывной случайной величины распо­ложены на всей оси x, то:

 

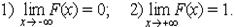
Функция распределения F(x) дискретной С.в. является ступенчатой, сохра­няющей постоянное значение на каждом интервале, не со­держащем точек x_i, и терпящей в этих точках скачок, рав­ный p_i.

Пример 2.24. Школьник дает ответы («Да» или «Нет») на 10 во­просов, причем вероятность поло­жительного ответа равна 0,5. По­стройте: а) закон распределения случайной величины, характери­зую­щей количество положительных ответов; б) функцию распределения этой случайной величины; в) найдите вероятность того, что школьник в серии из 10 вопросов даст менее 8, но больше 3 положи­тельных от­ветов.

Решение. а) Определим вероятность того, что в данном опросе школьник даст ровно 0, 1, 2, ..., 10 положительных ответов. Вероят­ность положительного ответа на вопрос обозначим как p = 0,5. Тогда вероятность отрицательного ответа составит q = 1 – p = 0,5. Рассмат­риваемое в задаче испытание удовлетворяет схеме Бернулли. Для на­шего примера вероятности положительного ответа ровно 0; 1; 2; ...; 10 раз равны: P₁₀(0) = C₁₀⁰p⁰q¹⁰ = 0,001; P₁₀(1) = C₁₀¹p¹q⁹ = 0,01; P₁₀(2) = C₁₀²p²q⁸ = 0,044; P₁₀(3) = C₁₀³p³q⁷ = 0,117; P₁₀(4) = C₁₀⁴p⁴q⁶ = 0,205; P₁₀(5) = C₁₀⁵p⁵q⁵ = 0,246; P₁₀(6) = C₁₀⁶p⁶q⁴ = 0,205; P₁₀(7) = C₁₀⁷p⁷q³ = 0,117; P₁₀(8) = C₁₀⁸p⁸q² = 0,044; P₁₀(9) = C₁₀⁹p⁹q¹ = 0,01; P₁₀(10) = C₁₀¹⁰p¹⁰q⁰ = 0,001.

Случайную величину (число положительных ответов в опросе из 10 вопросов) обозначим через X. События, состоящие в том, что слу­чайная величина X принимает каждое из возможных значений X=0, X=1, ..., X = 10, являются несовместными, т.к. случайная величина X может принимать в данной серии испытаний только одно значение. Следовательно, закон распределения данной случайной ве­личины в форме таблицы будет таким (см. рис. 2.5а).

Контроль: 0,001+ 0,01+ 0,044 + 0,117+ 0,205 + 0,246 + 0,205 + 0,117 + 0,044 + + 0,01 + 0,001 = 1.

б) Если x£0, то F(x)=0. Если 0 < x £ 1, то F(x)=0,001, т.к. X может принять значение 0 с вероятно­стью 0.001. Если 1 < x £ 2, то F(x) = P(x<2) = P₁₀(0) + P₁₀(1) = 0,011. Если 2< x£ 3, то F(x) = P(x<3) = P₁₀(0) + P₁₀(1) + P₁₀(2) = 0,055 и т.д. Следовательно, функция распределения имеет вид

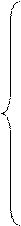0, если xÎ(-¥; 0];

0,001, если xÎ(0; 1];

0,011, если xÎ(1; 2];

0,055, если xÎ(2; 3];

0,172, если xÎ(3; 4];

0,377, если xÎ(4; 5];

F(x) = 0,623, если xÎ(5; 6];

0,828, если xÎ(6; 7];

0,945, если xÎ(7; 8];

0,989, если xÎ(8; 9];

0,999, если xÎ(9; 10];

1, если xÎ(10; +¥).

График функция распределения F (x) случайной величины показан на рис. 2.5б.

в) По следствию 1 из теоремы 2.16 P(3<X<8) = F(8) – F(3) = 0,945 – 0.055 = 0,89.

Ответ: в) 0,89.

 

X
P	0,001	0,01	0,044	0,117	0,205	0,246	0,205	0,117	0,044	0,01	0,001

а)

 

 

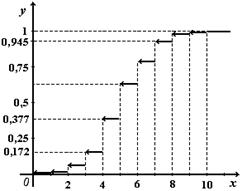б)

Рис. 2.5

Пример 2.25. Случайная величина задана X задана функцией рас­пределения

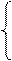0, если xÎ(-¥; -1];

F(x) = 0,25x + 0,25, если xÎ(-1; 3];

1, если xÎ(3; +¥).

Найти вероятность того, что в результате испытания X примет зна­чение, принадлежащее интер­валу (0; 2).

Решение. По следствию 1 из теоремы 2.16 P(0<X<2) = F(2) – F(0). Так как на интервале (0; 2) по условию F(x) = 0,25x +0,25, то F(2) – F(0) = (0,25·2+0,25) – (0,25·0+0,25) = 0,5.

Ответ: 0,5.

■ Плотность вероятности (плотность распределения веро­ятности) ( f(x) ) - это производная от функции распределения непрерывной С.в., т.е. f(x) = F¢ (x).

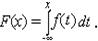В точках, где производная не определена, считают, что f(x) = 0. Ясно, что функция распределения

 

▲Теорема 2.18.Плотность вероятности неотрицательна, т.е. f(x)³0.

▲Теорема 2.19. Для непрерывной случайной величины X вероятность по­падания в промежуток с концами a и b (неважно, открытый или замкнутый) равна

P(a<X<b) = P(a£X£b) = F(b) – F(a) = 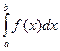.