III. Простейшие тригонометрические уравнения и неравенства.
.
Задание
Задание
Пусть дано выражение sin(p +a). Примените правило, чтобы записать правую часть:
sin(p + a) = ____________
 |
Примените правило для всех составленных примеров:
1)
2)
3)
4)
Докажем, тождество sin(p –a) = sina.
| Схема доказательства | Результат | ||||||
| 1. Построим на единичной окружности: a, p –a, М a, Мp –a, sina и sin(p –a) и сформулируем задачу на языке координат. | 
  
 
    Задача: доказать, что _________ точек М a, Мp –a равны Задача: доказать, что _________ точек М a, Мp –a равны
| ||||||
| 2. Проведем доказательство для знаков соответствующих координат. Докажем, что знаки соответствующих координат одинаковые (для других тождеств требуется доказать, что знаки являются противоположными). | Построенные точки лежат в одной полуплоскости относительно оси Ох, значит, их ____________________ имеют одинаковый знак. | ||||||
| 3. Докажем, что модули соответствующих координат одинаковые. | D __МaО = D __Мp–aО по _______________ и ________ углу a, значит, Мa__ = Мp–a___, т.е. модули ________________ равны. |
!!Самостоятельно доказать любую другую формулу приведения по той же схеме.
Пример 3. Четность-нечетность тригонометрических функций.
Верны следующие тождества:
sin(–a) = – sina (знак «минус» можно выносить из под знака синуса);
cos(–a) = cosa (знак «минус» можно опустить под знаком косинуса);
tg(–a) = – tga (знак «минус» можно выносить из под знака тангенса);
ctg(–a) = – ctga (знак «минус» можно выносить из под знака котангенса).
!!Самостоятельно доказать любое из перечисленных тождеств по той же схеме.
Способ 2. Равносильные преобразования верного равенства.
Пример 4. Тригонометрические тождества одного аргумента, которые можно доказать, используя основное тригонометрическое тождество.
Равносильное преобразование: деление обеих частей равенства на число, отличное от 0.
Если обе части основного тригонометрического тождества разделить на cos2х,
то получится тождество _______________________________________________
Пример 5. Формулы понижения степени.
Равносильное преобразование: замена выражения тождественно равным выражением.
Если в тождестве косинуса двойного аргумента выразить квадрат синуса через косинус по основному тригонометрическому тождество, то можно получить формулу понижения степени косинуса.
cos2х = _______________; cos2х = cos2х – (_________);
cos2х = ____________________; 2cos2х = _____________;
cos2х = 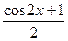
!!Самостоятельно доказать формулу понижения степени синуса.
Способ 3. Координатно-векторный метод.
Пример 6. Формула косинуса разности двух углов.
cos (a–b) = cos a cosb + sin a sinb
| Схема рассуждений | Результат | ||||||||||||
| 1. Построим на единичной окружности: a, b; М a, Мb; a – b и сформулируем задачу на языке координатно-векторном языке. |
 
  
  
    Задача: найти косинус угла между векторами ОМa, ОМb Задача: найти косинус угла между векторами ОМa, ОМb
| ||||||||||||
| 2. Найдем косинус угла между векторами ОМa, ОМb координатным способом | Вектор ОМaимеет координаты: (________);
Вектор ОМb имеет координаты: (________)
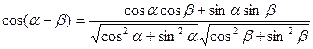 cos (a–b) = cos a cosb + sin a sinb
cos (a–b) = cos a cosb + sin a sinb
|
Способ 4. Сведение к известному.
Если a + b заменить на a – (–b), то можно использовать формулу тригонометрической функции разности аргументов.
Пример 7. cos (a + b) = cos (a – (–b)) = ___________________________________________.
Для доказательства формул двойного аргумента 2a заменяют a + a и применяют формулу тригонометрической функции суммы аргументов.
Пример 8. cos 2a = cos (a + a) = ___________________________________________.
Если sina заменить на cos (p/2 – a), то можно использовать формулу, доказанную для косинуса; если cos a заменить на sin (p/2 – a), то можно использовать формулу, доказанную для синуса.
Пример 9. sin (a + b) = cos (p/2 – (a + b)) = ________________________________________
_______________________________________________________.
Если a – b заменить a + (–b), то можно использовать формулу тригонометрической функции суммы аргументов.
Пример 10. sin (a – b) = sin (a + (–b)) = ___________________________________________.
Для доказательства формулы произведения тригонометрических функций используют сложение (вычитание) известных тождеств о тригонометрической функции суммы и разности аргументов.
Докажем, например, тождество, в котором участвует произведение синусов.
| Схема рассуждений | Результат |
| 1. Произведение синусов участвует в формулах косинуса суммы, косинуса разности. Запишем эти тождества. | cos (a – β) = ______________________ cos (a + β) = _______________________ |
| 2. Чтобы «подобраться» к произведению синусов, вычтем из первого равенства второе. | cos (a – β) – cos (a + β) = _______________ |
| 3. Выразим из полученного равенства нужное произведение. | sina sin β = __________________________ |
!!Самостоятельно доказать по той же схеме любое тождество из группы произведения тригонометрических функций.
Способ 4. Введение новых переменных.
Формулы суммы (разности) тригонометрических функций доказываются с введением новых переменных.
| Схема рассуждений | Результат |
| 1. Сумма тригонометрических функций участвует в формулах произведения тригонометрических функций. Выберем нужную формулу. | Пусть требуется найти сумму синусов. Выберем формулу:
sina cos β = 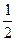 ( sin (a + β) + sin (a – β)) ( sin (a + β) + sin (a – β))
|
2. Введем новые переменные:
a + b = х;
a – b = у.
Тогда надо выразить a и b через новые переменные.
Сложение равенств дает _____ = ______; вычитание равенств дает _____ = ______;
откуда:  , , 
|
sin____cos ______= 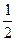 ( sin ___ + sin ____) ( sin ___ + sin ____)
|
| 3. Выразим из полученного равенства нужную сумму | sin х + sin у = ________________ |
!!Самостоятельно доказать по той же схеме любое тождество из группы суммы (разности) тригонометрических функций.
Простейшие тригонометрические уравнения sinx = a; cosx = a; tgx = a; ctgx = a, если имеют решения, то их бесконечно много. Возникает проблема, как записать все решения?
Договорились, для одного корня уравнения ввести специальное обозначение, а другие корни – выразить через него.
Определение. Арксинусом числа а называется такое число из промежутка [–p/2; p/2], синус которого равен а. Обозначение: arcsinа.
Определение. Арккосинусом числа а называется такое число из промежутка [0; p], косинус которого равен а. Обозначение: arcсosа.
Определение. Арктангенсом числа а называется такое число из промежутка (–p/2; p/2), тангенс которого равен а. Обозначение: arctgа.
Определение. Арккотангенсом числа а называется такое число из промежутка (0; p), котангенс которого равен а. Обозначение: arcctgа.
Выведем формулы решения уравнений sinx= a и cosх = а.
Схема: 1) выделим случаи: нет решений; основной; частные; 2) выведем формулу для основного случая: промежуток длиною в период, основной корень – арк; второй корень через основной; две серии корней с учетом периодичности; объединение корней в одну формулу; 3) частные случаи без использования основной формулы.

 На [–p/2; 3p/2] А: х = arcsina
В: х =p– arcsina
На всей области определения:
А: х = arcsina + 2pп, пÎZ
В: х = –arcsina+ (2p+1)п, пÎZ
Объединение: х = (–1)karcsinа+ pk, kÎZ
На [–p/2; 3p/2] А: х = arcsina
В: х =p– arcsina
На всей области определения:
А: х = arcsina + 2pп, пÎZ
В: х = –arcsina+ (2p+1)п, пÎZ
Объединение: х = (–1)karcsinа+ pk, kÎZ
 а = 0.
х = _____________, пÎZ
а = 0.
х = _____________, пÎZ
 а = 0
х = _____________, пÎZ
а = 0
х = _____________, пÎZ