Поквартальная продажа мяса в течение шести лет по Ивановскому району, млн. руб.

Исчисление средней сезонной волны из процентных отношений уровней

Годы   Среднеквартальный уровень продажи, млн. руб.   Процентные отношения уровней ряда к среднеквартальным уровням  
I   II   III   IV  
А            
Сезонная волна в среднем за 6 лет   55,81 47,84 49,77 49,22 40,70 43,81   92,94 100,31 86,44 94,05 98,35 83,35   92,57   98,46 101,86 99,70 97,50 98,65 89,69   97,64   111,65 100,40 117,42 116,15 116,31 131,37   115,54   96,97 97,43 96,44 92,28 86,71 95,64   94,25  

 

Сезонная волна, исчисляется из процентных отношений уров­ней ряда, более правильно отражает сезонные колебания (при нали­чии небольшой тенденции), чем сезонная волна, вычисленная по методу средней арифметической непосредственно из уровней ряда, ибо процентные преобразования несколько снижают влияние общей тенденции развития на сезонную волну.

Метод простой средней, при всей несложности его вычислений, являющейся его достоинством, для анализа сезонных колебаний применяется редко даже при некоторых его усовершенствова­ниях, поскольку он не может исключить влияние общей тенденции, а уровень явлений в большинстве случаев имеет выраженную тенденцию подъема или снижения и почти никогда не остается постоянным на протяжении изучаемого периода.

2. Метод относительных чисел. Этот метод применяется для анализа сезонности тех рядов динамики, развитие общей тенденции которых происходит равномерно. Порядок расчета сезонной волны методом относительных чисел рассмотрим на примере.

Пример. Провести анализ методом относительных чисел сезонной реализации мяса поквартально по Ивановскому району по шести годам.

Порядок расчета сезонной волны методом относительных чисел рассмотрим на примере данных табл. 9.15. Для исчисления цепных отношений предварительно располагаем данные поквартальной продажи по годам.

 

Таблица 9.15

 

Годы   Поквартальные продажи мяса   Итого за год  
    I кв.   II кв.   III кв.   IV кв.  
А            
  44,7   43,2   44,7   54,6   187,2  
  55,3   44,5   43,4   51,5   194,7  
  51,9   40,1   41,5   55,9   189,4  
  54,3   46,7   43,8   59,8   204,4  
  57,9   48,7   44,9   60,0   211,6  
  60,7   51,0   51,7   69,0   232,4  

 

Цепные отношения вычисляются как процентные отношения объемов продажи за каждый квартал к объему продажи предшествующего квартала, в результате получается система относительных чисел, связанных в цепь. Далее из относительных чисел вычисляется простая средняя величина для каждого квартала за все шесть лет. Затем средняя за первый квартал приравнивается к единице (или 100), а средние за остальные кварталы определяются по методу цепных произведений. Таким образом, если средний уровень первого квартала будет 100, то во втором квартале он будет равен 84,75, в третьем — 83,60, в четвертом — 108,56.

 

Таблица 9.16

Анализ методом относительных чисел сезонности продажи мяса по данным табл. 9.14

Годы     Поквартальные процентные от- ношения уровней ряда   Средние из квартальных отношений за год  
I кв.   II кв.   III кв.   IV кв.  
               
А            
  —   96,64   103,47   122,15   107,42  
  101,28   80,47   97,53   118,66   99,49  
  100,78   77,26   103,49   134,70   104,10  
  97,14   86,00   93,79   136,53   103,37  
  96,82   84,11   92,20   133,63   101,69  
  101,17   84,02   101,37   133,46   105,01  
Среднеквартальные отношения из цепных отношений за шесть лет Преобразованная средняя Преобразованная и исправленная средняя Сезонная волна в среднем за шесть лет                      
    99,44   100,00     98,01   109,8       84,75   84,75     80,78   90,5              
  98,64   83,60     77,64   86,9     129,86   108,56     100,61   112,8     —   —     89,26   100,00  

 

При отсутствии общей тенденции подъема или снижения произведение преобразованной средней за IV квартал на сред­нюю из цепных отношений первого квартала дает первона­чальный уровень преобразования средней, т.е. 100,00; оно будет более 100, если наблюдается общая тенденция увеличения и, напротив, менее 100, если наблюдается общая тенденция уменьшения. Расхождение между произведением преобразованной средней за IV квартал на среднюю из цепных отношений первого квартала и 100,00 — погрешность, возникшая в результате повышающейся или понижающейся общей тенденции, эту погрешность необходимо устранить. Наиболее простой способ устранения погрешности состоит в равномерном распределении ее на все кварталы. В нашем примере под влиянием растущей общей тенденции сезонные коле­бания оказались сдвинутыми на 7,95% (108,56 • 99,44 = 107,95). Для получения исправленных сезонных колебаний необходимо из показателей первого квартала вычесть 1/4 от 7,95 из 100, получается 98,01; для второго квартала вычесть 2/4 от 7,95 из 84,75, будет 80,78; для третьего квартала надо вычесть 3/4 от 7,95 из 83,60 (преобразованной для III кв. средней), получим 77,64 и для четвертого квартала надо вычесть 4/4 от 7,95 из 108,56, получится 100,61. Далее исчисляется средняя квартальная, как средняя арифметическая из преобразованных и исправленных квартальных средних .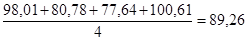

Сезонная волна в среднем за весь период исчисляется как про­центное отношение преобразованных и исправленных средних за каждый квартал к их общей средней. Для первого квартала, например, она будет равна 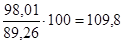; для второго квартала — ; для третьего квартала — 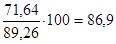и для четвертого квартала —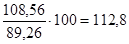

Таблица 9.16 показывает сезонность продажи, максимум про­дажи приходится на четвертый квартал, а минимум — на третий. На протяжении шести лет в четвертом квартале продавалось мяса на 12,8% (112,8 - 100) больше среднеквартальной продажи, а в третьем квартале в среднем на 13,1% меньше.

Метод исчисления сезонных колебаний способом относительных чисел точнее метода простой средней, так как с его помощью исключается влияние общей тенденции подъема (снижения) уровней ряда динамики на сезонную волну в среднем за весь изучаемый период, однако и этот метод не лишен недостатков. Один из его недостатков — механическое внесение относительно одинаковой поправки в анализируемые отрезки времени, которое означает признание равномерного развития уровней явления.

3. Анализ сезонности методом У. Персонса. Данный метод применяется в рядах динамики, отражающих развитие явлений, об­щая тенденция которых изменяется по средней геометрической, т.е. по сложным процентам. Суть метода У. Персонса заключается в исчислении показателей средней сезонной волны как медианных значений (а не как простых средних арифметических) из цепных отношений. Здесь погрешность, вызываемая влиянием общей тенденции, устраняется с помощью среднего коэффициента подъема (снижения) общей тенденции по средней геометрической. Для анализа этим методом сначала, как и в методе относительных чисел, необходимо вычислить цепные отношения как процентные отноше­ния каждого уровня ряда к уровню ряда предшествующего, но потом исчислять средние не как средние арифметические, а как медианные значения. Медиана за первый отрезок времени принимается за единицу (или 100), а для остальных периодов средние исчисляются путем последовательного перемножения медианных средних. При перемножении преобразованного медианного значения за четвертый квартал на медианные значения первого квартала должна получиться единица (100,00). Однако результат обычно бывает больше единицы или меньше ее, поскольку он отражает действительность, на развитие которой оказывает влияние общая тенденция увеличения или уменьшения.

При анализе сезонности методом относительных чисел разность теоретического и действительного включалась равномерно из каждого квартального показателя, в способе У. Персонса исключение разности основано на применении формулы сложных процентов.

Исчислим сезонную волну по этому методу, используя данные табл. 9.16 о поквартальных продажах мяса по Ивановскому району за шесть лет. Сначала нужно исчислить цепные отношения, они уже нами определены (табл. 9.16), затем определяем среднеквартальные показатели как медианные значения из цепных отношений уровней продажи, расположенных по возрастающим значениям, а не по значениям времени возникновения. Для первого квартала ранжированный ряд данных отношений будет иметь вид: 96,82; 97,14; 100,78; 101,17; 101,28; медиана этого ряда — 100,78 — центральный член нечетного числа членов ряда. Ранжированный ряд цепных отношений второго квартала: 77,26; 80,47; 84,02; 84,11; 86,00; 96,64; медиана этого ряда — средняя двух центральных членов ряда четного числа членов: 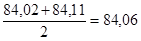. Таким же образом исчисляются медианные значения для третьего и четвертого кварталов из их цепных отношений.

Медианные значения исчисляются из цепных отношений, ко­торые необходимо преобразовать в базисные, приняв за основу ме­диану первого квартала. Значение для второго квартала в отноше­нии к первому уже было установлено — 84,06%, для третьего квар­тала оно определяется перемножением показателя второго квартала на медианное значение из цепных отношений третьего квартала: 84,6 • 99,45: 100 = 83,60 и т.п.

Перемножение преобразованного значения за четвертый квартал на медианное значение первого квартала (111,6 • 100,78 = 112,51) обнаруживает, что под влиянием возрастающей общей тенденции развития ряда динамики сезонные колебания сдвинулись на +12,51% (112,51 - 100,00).

 

Таблица 9.17