Фактические и выравненные значения урожайности зерновых фермерского хозяйства
Данные об урожайности зерновых в фермерском хозяйстве и расчет по ним выравнивания динамического ряда, центнеров с га
| Годы | Урожай (у) | х | х2 | ух | 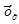
|
| 8,5 | -1 | -59,5 | 8,74 | ||
| 8,7 | -5 | -48,5 | 9,10 | ||
| 8,3 | -3 | -24,9 | 9,46 | ||
| 10,5 | -1 | -10,5 | 9,82 | ||
| 10,4 | +1 | 10,4 | 10,18 | ||
| 11,4 | +3 | 34,2 | 10,54 | ||
| 9,2 | +5 | 46,0 | 10,90 | ||
| 12,0 | +7 | 84,0 | 11,26 | ||
| Сумма | 80,0 | 31,2 | — |
По приведенным выше формулам найдем а0 = 10,00 и а1 = 0,18. Уравнение прямой будет 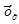 = 10.00+ 0.18t. Таким образом, выравненный по прямой динамический ряд урожайности зерновых фермерского хозяйства будет: 1993 год — 8,74 ц; 1994 год — 9,74 ц; 1995 год — 9,46 ц; 1996 год — 9,82 ц; 1997 год — 10,18 ц; 1998 год — 10,54 ц; 1999 год — 10,90 ц; 2000 год — 11,26 ц. Изобразим фактические и выравненные значения на схеме 9.1.
= 10.00+ 0.18t. Таким образом, выравненный по прямой динамический ряд урожайности зерновых фермерского хозяйства будет: 1993 год — 8,74 ц; 1994 год — 9,74 ц; 1995 год — 9,46 ц; 1996 год — 9,82 ц; 1997 год — 10,18 ц; 1998 год — 10,54 ц; 1999 год — 10,90 ц; 2000 год — 11,26 ц. Изобразим фактические и выравненные значения на схеме 9.1.
Схема 9.1

Параболическое выравнивание динамического ряда — это нахождение плавного уровня ряда в предположении его изменения по параболе (по кривой п - го порядка). Уравнение кривой 2-го порядка: у = а + а1х + а2х2. Уравнение кривой 3-го порядка: у = а0 + а1х + а2х2 + а3х3. Уравнение кривой п-го порядка: у = а0 + а1х + а2х2 +... + апхп. Параболическое выравнивание сводится по существу к определению параметров кривой а0,а1,а2...ап. Для этого при применении способа наименьших квадратов необходимо решить систему нормальных уравнений.
Так, например, для выравнивания по кривой 2-го порядка у = а + а1х + а2х2система нормальных уравнений имеет вид:
{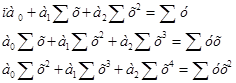
Число уравнений зависит от степени свободы (п) кривой. Так, для определения параметров уравнения параболы необходимо решить систему трех уравнений с тремя неизвестными, для определения параметров уравнения кривой 3-го порядка — систему четырех уравнений с четырьмя неизвестными и т.д. В решении вопроса о применимости выравнивания параболического по параболе того или иного порядка существенную помощь оказывает метод конечных разностей.
Конечные разности — это соотношение вида:
 - разность первого порядка
- разность первого порядка
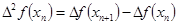 - разность второго порядка
- разность второго порядка
 - разность k - го порядка
- разность k - го порядка
где хп = х0 + пh; h - постоянно, п - целое число. Конечные
разности исследуют функции при прерывном значении аргумента. Например, полагая, что разность двух последовательных значений х равна 1, и имея значения функции f(х), получим следующие конечные разности.
Таблица 9.1