Аналитическое выравнивание динамического ряда по прямой
Аналитическое выравнивание динамического ряда
Выравнивание по прямой — это нахождение плавного уровня ряда в предположении его изменения по прямой:
 , где
, где 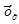 — уровень, найденный по уравнению; а0 и а1 — параметры уравнения, которые при применении способа наименьших квадратов находятся из решения системы нормальных уравнений; х — время или иной аргумент.
— уровень, найденный по уравнению; а0 и а1 — параметры уравнения, которые при применении способа наименьших квадратов находятся из решения системы нормальных уравнений; х — время или иной аргумент.
Нормальные уравнения служат для отыскания параметров при выравнивании по прямой, выравнивании параболическом, нахождении корреляционного уравнения и т.д. Для выравнивания по прямой  , система нормальных уравнений принимает вид:
, система нормальных уравнений принимает вид:
{
Выравнивание по прямой применяется в том случае, когда возрастание уровня ряда динамики в среднем сохраняет постоянство абсолютных приростов. Однако ввиду простоты расчета параметров уравнения и в других случаях применяется выравнивание по прямой.
При  п — число членов ряда.
п — число членов ряда.
Пример. Урожайность зерновых в фермерском хозяйстве представлена следующим рядом динамики, который мы выравниваем по прямой.
Таблица 9.9