Расчет медианы по интервальному ряду

 

Группы семей по среднемесячному доходу на 1 человека, руб.	Число семей
До 900 900—1200 1200—1500 1500—1800 Свыше 1800
ИТОГО

 

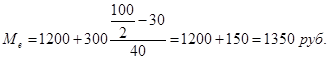
Следовательно, 50% семей имеют доход на одного человека <1350 руб., а 50% имеют доход на одного человека >1350 руб.

У медианы есть свойство, которое заключается в том, что сумма абсолютных величин линейных отклонений от М_е минимальна.

 

Это свойство очень важно при практическом применении медианы.

Пример. Филиалы торговой фирмы «Элегант» расположены на расстоянии 10, 30, 70, 90, 100 км от нее. Где построить склад фирмы для оптимального снабжения филиалов?

М_е=70 км.

 

Таблица 5.10

Расчетная таблица для сравнения отклонений от медианы и от средней арифметической

 

Расстояние, км	|х-Ме|	|х-|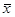
	-60 -40 +20 +30	-50 -30 +10 +30 +40
ИТОГО	±150	±160

 

Таким образом, оптимальным вариантом является медианное расстояние 70 км, так как 150 < 160 км на 40 км.

Подводя итог рассмотрению моды и медианы особо следует отметить, что данные два показателя часто используются вместо средней арифметической или вместе с ней. Так, например, фиксируя цены на продукты на мелкооптовых рынках, записывают наиболее часто встречающуюся цену каждого продукта, т.е. моду цены. Од­нако наилучшей характеристикой величины варианта или уровня ряда служит средняя арифметическая, которая имеет ряд преиму­ществ, главное из них — точное отражение суммы всех значений признаков, необходимой для решения ряда практических задач.

Вместе с тем для тех случаев, когда в совокупности имеется небольшое число единиц с чрезмерно большим или чрезмерно ма­лым значением исследуемого признака, в дополнение к средней арифметической целесообразно исчислять моду и особенно медиа­ну, которые, в отличие от средней, не зависят от этих крайних, не характерных для совокупности значений признаков.