Средняя гармоническая

 

Средняя гармоническая применяется в тех случаях, когда частоты (веса) не приводятся непосредственно, а входят сомно­жителями в один из имеющихся показателей.

Пример. Автомобиль доставил товары в три магазина фирмы «Весна», которые удалены от головного предприятия на одинаковое расстояние. Так, до первого магазина, расположенного на шоссей­ной дороге, автомобиль прошел путь со скоростью 50 км/час, до второго, по проселочной дороге, — 40 км/час, а в третьем случае автомобилю пришлось полпути пройти через лесной массив, и ско­рость движения составила только 30 км/час.

Требуется определить среднюю скорость движения автомоби­ля. На первый взгляд представляется, что средняя скорость движе­ния может быть определена по формуле простой арифметической:

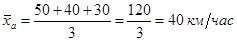
Однако нетрудно убедиться, что средняя вычислена неправильно. В самом деле, производя расчет средней скорости по простой арифметической средней, исходим из того, что автомобиль во всех трех случаях прошел одинаковое расстояние, пройдя соответственно 50, 40 и 30 км, т.е. всего 120 км. Если бы условие этой задачи было сформулировано в такой форме, то средняя была бы рассчитана правильно и характеризовала бы пройденное автомобилем среднее расстояние.

В действительности же эта средняя рассчитана неверно, так каш из условия задачи не следует, что автомобиль на преодоление расстояния до трех магазинов фирмы «Весна» проехал 120 км, так как скорость движения была различная. Следовательно, он прошел и разное расстояние.

В подобных случаях нужно применить формулу средней гармонической простой (не взвешенной):

или в сокращенном виде

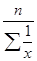
где 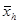— средняя гармоническая;

- числа, обратные заданным вариантам.

Иначе говоря, простая гармоническая средняя есть отноше­ние числа вариантов к сумме обратных значений этих вариантов.

Для нашего примера будем иметь:

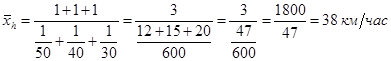
В нашем примере средняя арифметическая оказалась больше средней гармонической .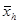

При этом абсолютная ошибка завышения составляет 2 км/час (38 - 40), а относительная — 5% .

Таким образом, неправильное использование арифметической средней привело бы к завышению средней скорости движения авто­мобиля и может привести к неправильному определению объема перевозок.

Это еще раз доказывает, с какой осторожностью следует решать вопрос о том, какую среднюю надлежит применять в экономических расчетах.

В рассмотренном примере частоты (веса) имели одно значение и равнялись единице. Если же частоты (веса) различные, то применяется средняя гармоническая взвешенная, которая вычисляется следующим образом:

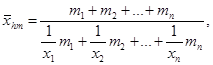
где — средняя гармоническая взвешенная, или

 

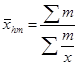
Как первая, так и вторая формула показывают, что средняя гармоническая есть величина обратная средней арифметической.

Веса арифметической средней и гармонической средней обозначены разными буквами: f и т. Это не случайно, также весами средней арифметической служат частоты рассматриваемого ряда, а весами гармонической средней будет произведение вариантов на веса.

Пример. Рассмотрим данные о реализации товаров по двум магазинам фирмы «Весна».

Таблица 5.6

Данные о реализации товаров по двум магазинам фирмы «Весна»

 

Магазины	Цена товара (х), руб.	Количество реали­зованного товара (f), кг	Товарооборот (т=х f), руб.
А
№1 №2	20,0 18,0		50 000 72 000
ИТОГО	—		122 000

 

Из условия задачи видно, что количество реализованного товара принимается за вес, который обозначается через букву f. Товарооборот — произведение цены на количество товара: полученный таким образом вес обозначается через т.

Для определения средней цены реализованного товара, исходя из условий задачи, можно применить в одном случае арифметиче­скую, в другом — гармоническую взвешенную. Если при вычисле­нии средней цены в качестве веса брать количество проданного то­вара (f), то решение производят по арифметической взвешенной:

Если же в качестве веса используется товарооборот (т), для расчета средней цены нужно применить среднюю гармоническую:

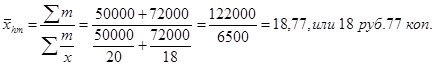
Следовательно, выбор формулы средней (гармонической или арифметической) зависит от так называемого определяющего пока­зателя.

Определяющим показателем называется показатель, кото­рый получает реальное экономическое значение при умножении вариантов на веса или при делении весов на варианты. В нашем примере в первом случае при перемножении вариантов на веса (хf) получается сумма товарооборота, т.е. реальная экономическая вели­чина. Поэтому для расчета средней цены применяют среднюю арифметическую взвешенную.

Во втором случае перемножение вариантов на веса (хт), т.е. цены товара на товарооборот, никакого реального показателя не дает, а получается бессмыслица. Поэтому во втором случае веса делят на варианты . Частное от деления товарооборота на цену показывает количество реализованного товара и имеет реальный экономический смысл. В этом случае применяется средняя гармоническая взвешенная.