Средняя хронологическая

Свойства средней арифметической

Рассмотрим основные свойства средней арифметической.

Первое свойство. Нулевое свойство средней величины заклю­чается в том, что сумма отклонений вариант от их средней арифме­тической величины равна нулю.

Первое свойство средней может быть использовано, в частно­сти, для контроля правильности вычислений арифметической сред­ней: если средняя вычислена правильно, сумма отклонений должна равняться нулю (практически, с учетом округлений, допускаемых при вычислении средней, — очень близка к нулю).

Второе свойство. Если все варианты уменьшить или увеличить на одно и то же постоянное число, то средняя арифметическая из этих вариант уменьшится или увеличится на то же самое число.

Пример. Пусть заработная плата каждого работника фирмы «Весна» увеличилась за некоторый период на 150 руб. Тогда сред­няя заработная плата всех работников фирмы увеличилась также на 150руб.

Третье свойство. Если все варианты одинаково увеличить (или уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (или уменьшится) во столько же раз.

Пример. Так, если бы заработная плата каждого работника фирмы «Весна» увеличилась на 10%, то и средняя заработная плата всех работников фирмы увеличилась бы на 10%.

Четвертое свойство. Если же все веса средней одинаково уве­личить (или уменьшить) в несколько раз, средняя арифметическая не изменится.

Увеличение всех весов в несколько раз приводит к тому, что во столько же одновременно увеличится и числитель, и знаменатель дроби (средней арифметической), поэтому значение дроби не изме­няется.

 

Средняя хронологическая — это средний уровень ряда ди­намики, т.е. средняя, исчисленная но совокупности значений показателя в разные моменты или периоды времени. В зависи­мости от вида ряда динамики применяются различные способы ее расчета, а именно расчет: средней хронологической интервального ряда; средней хронологической моментного ряда.

Средней хронологической интервального ряда является средняя величина из уровней интервального ряда динамики и исчисляется по формуле:

где 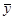— средний уровень ряда;

у — уровень ряда динамики;

п — число членов ряда.

Средней хронологической моментного ряда является сред­няя величина из уровней моментного ряда динамики. Если f(t) есть функция, выражающая изменение моментного показателя во времени, то за время (t) от а до b средняя хронологическая момент­ного ряда равна:

Однако данных непрерывного наблюдения значения f(t) в распоряжении статистики, как правило, нет. Поэтому в зависимости от характера изменения показателя и имеющихся данных применяются различные методы расчета. При равных промежутках времени между датами, на которые имеются данные, и равномерном изменении размера показателя между датами средняя хронологическая моментного ряда обычно исчисляется по формуле:

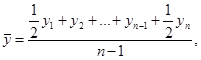
у — уровень ряда;

п — число всех членов ряда;

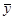— средний уровень.

Если периоды времени, отделяющие одну дату от другой, не равны между собой, то расчет средней хронологической моментного ряда производится по формуле средней взвешенной арифметиче­ской, в качестве весов которой принимаются отрезки времени между датами, т.е. по формуле:

где Т — время, в течение которого данный уровень ряда (у) оставался без изменения.

Известно, например, что в январе 2001 года произошло сле­дующее изменение численности сотрудников компании «Бест»: бы­ло на 1 января 551 чел., уволился 2 января один сотрудник, было принято 6 января 24 человека, 16 января — 6 человек, уволилось 25 января — 10 сотрудников. Требуется определить среднюю числен­ность сотрудников компании «Бест» в январе 2001 г. Рассчитаем число календарных дней, в течение которых численность сотрудни­ков компании «Бест» оставалась без изменения, и произведение этих чисел.

Таблица 5.5

Данные для расчета средней численности сотрудников компании «Бест»

 

Численность сотрудников компании «Бест», чел. (у)	Число календарных дней, в течение которых данная численность сотрудников оставалась без изменения (Т)	Произведение численности сотрудников на число календарных дней (уТ)
ИТОГО

 

Используя данные произведенных расчетов, получим:

В отличие от первого способа расчета средней хронологиче­ской моментного ряда второй способ дает точное значение средней.