Расчет средней арифметической по данным интервальной группировки

Распределение магазинов фирмы «Весна» по торговой площади

 

Площади магазинов — варианты (х), кв. м
							Всего
Удельный вес численности магазинов в общей численности (f), %

Тогда

где x_af — средняя арифметическая взвешенная.

Следовательно, теперь получится та же величина средней, од­нако вместо частот будут использованы удельные веса (частости).

 

Предположим, требуется вычислить средний размер товаро­оборота предприятий общественного (массового) питания по муни­ципальному округу «Ломоносовский» (г. Москва).

Как видно из данных табл. 5.3, варианты носят интервальный характер, т.е. имеют не точное, а только приблизительное значение. В этих случаях, чтобы вычислить общую среднюю, необходимо найти середину, т.е. центральное значение каждого интервала. Однако первый и последний интервал даны открытыми: в первом отсутствует нижняя граница, в последнем — верхняя.

Исчисление средних по данным интервальных рядов с закрытыми интервалами производится по формуле средней арифметиче­ской простой, т.е. для второго интервала 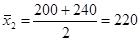тыс. руб. (расчеты показаны в табл. 5.4).

Для фирм массового питания с оборотом до 200 тыс. руб. ус­ловно считаем, что этот интервал равен последующему, т.е. 40 тыс. руб. (240 - 200), затем от 200 тыс. руб. вычитаем 40 тыс. руб. и на­ходим нижнюю границу первого интервала, которая будет равна 160 тыс. руб. (200 - 40). Затем расчет ведется так же, как и для вто­рой группы, т.е. по формуле средней арифметической простой.

 

Таблица 5.4