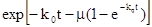Кинетика тушения люминесценции в мицеллярных растворах.

Одной из немногих точно решаемых кинетических задач в мицеллярных растворах является частный случай химической реакции, когда один из реагентов находится в большом избытке, так что его расходом в ходе реакции можно пренебречь. Например, этому условию точно удовлетворяет процесс тушения люминесценции возбужденной молекулы-люминофораL* молекулой тушителя.

L* + Q ® L + Q*

В этом случае уравнения (2.4) существенно упрощаются, так как m_Q = m = const, m_L* <<1 и вместо двухиндексной функции распределения (2.3) вводится одноиндексная функция распределения P*_n(t) – относительная доля мицелл, содержащих n молекул тушителя Q и одну возбужденную молекулу люминофора L*.

Теперь перейдем к задаче о кинетике тушения флуоресценции, т.е. будем считать, что кроме молекул Q в мицеллярном растворе находятся еще и молекулы люминофора L. Обозначим через M_nj - число мицелл, содержащих n молекул тушителя Q и l молекул люминофора L, а через P_nl = Mnl/M соответствующую функцию совместного распределения молекул люминофора и молекул тушителя по мицеллам.

 

Q = Q_s + m_qM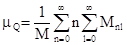

 

L = L_s + m_lM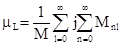

 

Задача тушения флуоресценции сводится к рассмотрению кинетики изменения концентрации возбужденных молекул после действия короткого импульса света, или как принято говорить d - импульса. Пусть a - доля возбужденных молекул в начальный момент времени, сразу после действия d - импульса.

Для a << 1 можно считать, что все мицеллы можно разделить на два класса, содержащие и несодержащие возбужденную молекулу люминофора. Предположим, что по какой-то причине возбужденная молекула люминофора не покидает своей молекулы. Тогда все элементарные процессы можно представить следующей схемой

 

 

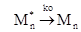
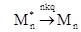
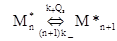
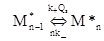
Если ввести Pn^* (t) - вероятность найти возбуждение в момент времени t в мицелле, содержащей n тушителей, то можно записать следующую систему кинетических уравнений

 

 

……………………………………

 

……………………………………………………..

 

 

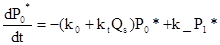
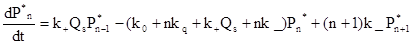
Также можно ввести производящую функцию G^*(s,t) и получить уравнение

 

 

 

 

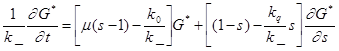
Далее решая это уравнение при условии, что начальное распределение является распределением Пуассона, можно получить

 

P^*(t)=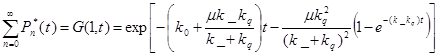

 

Частный случай отсутствия миграции тушителей (k=0) дает формулу

 

P (t) =