Точки, в которых интенсивность имеет наименьшее значение, называются интерференционными минимумами. Там, где энергия наиболее велика, располагаются интерференционные максимумы.
В повседневной жизни явление интерференции, как правило, не наблюдается, т.к. обычные источники света некогерентные. Получить когерентные световые волны можно только искусственным путем, например, разделением волны, испускаемой одним источником, на две части, которые потом накладываются друг на друга (метод Юнга, зеркало Ллойда, бипризма Френеля и т.д.). Второй путь – использование специальных источников света – лазеров.
Определим условия образования интерференционных максимумов и минимумов. Для общности вывода предположим, что волны после разделения распространяются в разных средах (рис.4). До точки М, в которой происходит наложение когерентных волн, одна волна в среде с показателем преломления n1 прошла путь s1, а вторая – в среде с показателем преломления n2 – путь s2. В соответствии с (1) первая волна возбудит колебание
, а вторая 
, где υ1 = с/n1 и υ2 = с/n2 фазовые скорости волн, соответственно, в первой и второй среде.
Разность фаз колебаний, возбуждаемых волнами вида (1) в точке М:
Δφ = φ2 - φ1=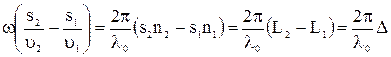 
. (11)
Величины L1= s1n1 и L2 = s2n2 называются оптической длиной пути, а величина Δ = L2 - L1 - оптической разностью хода двух волн.
Т.к. max возникает в точках, для которых соs δφ = 1, а это, как известно, выполняется для всех δφ = 2kπ(k = 0, ±1, ±2, …), то мы можем записать для максимумов:
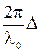= 2kπ или Δmax = 2k
. (12)
Это означает, что во всех точках, для которых разность хода двух когерентных волн равна нулю или четному числу полуволн будет наблюдаться интерференционный максимум. Совокупность таких точек с одним и тем же значением k образует линию максимума k-го порядка.
Для интерференционных минимумов аналогично получим: т.к. соs δφ = 0в случае, если δφ = (2k+1) π,где k = 0, ±1, ±2, …, то:
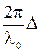= (2k + 1)πили Δmin = (2k + 1). (13)
Совокупность точек с постоянным значением k образуют линии интерференционных минимумов k-го порядка, которые располагаются между линиями соответствующих максимумов.