Выразим текущее количество теплоты, которой обмениваются внешний источник и рабочее тело, в виде

, (1)

где - общее количество теплоты, участвующей в процессе, х – характеристика теплообмена.

Рассмотрим задачу определения х в общем виде.

Параметры газа находятся путём решения уравнения первого закона термодинамики, выраженного в дифференциальной форме:

. (2)

Здесь: dQ, dV и dT – дифференциалы, соответственно, теплоты, объёма и температуры газа, М – количество молей газа, – истинная мольная теплоёмкость, p – давление.

Введём понятие относительного объёма v и удельной теплоты процесса , полученных путём отнесения абсолютных объёма V и теплоты Q₀ к какому-либо объёму , например, к начальному, конечному или промежуточному, являющемуся характерным для данного процесса.

Достаточным условием для решения (2) в элементарных функциях является выражение относительной интенсивности теплообмена w = dx/dv в виде ряда . Интегрируя выражение w при к = 1, получим искомую величину х.

Текущее значение характеристики теплообмена равно

. (3)

Индексы 1 и 2 соответствуют относительным объёмам в начале и конце процесса, отсутствие индекса - текущему объёму.

Интенсивность теплообмена

. (4)

Зависимость протекания характеристик х от относительного объёма для разных значений показателя характеристики m приведена на рис. 3.

Формы кривых определяются величиной и знаком показателя m, а также направленностью процесса – сжатием или расширением.

В обоих случаях при m = 0 значение х линейно зависит от объёма. Подвод теплоты осуществляется мгновенно при объёме v₁ для m = +при расширении и для при сжатии. В случае противоположных знаков показателя m мгновенный подвод теплоты осуществляется при объёме v₂.

Однонаправленный термотропный процесс для идеального газа рассматривается при постоянном отношении теплоёмкостей k и только для процессов сжатия или расширения.

Параметры процесса. Запишем дифференциальное уравнение первого закона термодинамики в виде

, (5)

где q₀ = Q₀ / V_хар - удельная теплота процесса, отнесённая к характерному для данного процесса объёму V_хар, k – отношение истинных теплоёмкостей газа при постоянных давлении и температуре газа (коэффициент адиабаты), 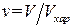- относительный объём, р – давление.

Зависимости (3) и (4) справедливы для однонаправленных процессов, представляющих собой только сжатие или только расширение.

Подстановка (4) в (2) и последующее интегрирование позволяет получить выражения текущего давления однонаправленного процесса для случая постоянного отношения теплоёмкостей (коэффициента адиабаты) k

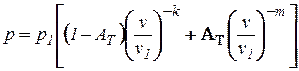, (6)

где безразмерный параметр , (7) Здесь - коэффициент использования теплоты процесса, равный доле теплоты топлива, используемой на изменение внутренней энергии и работу.

Текущие температуры здесь определяются по уравнению состояния

,

Относительные объёмы, при которых наступают максимальные значения давления и температуры процесса равны:

, (8)

. (9)

Текущая удельная работа процесса, отнесённая к базовому объёму,

. (10)

В ДВС максимальные температуры и давления при сгорании располагаются на линии расширения, при этом для реальных процессов 1,5 < m < 7.