Адиабатный процесс (закон Пуассона, 1823 г.).

(французский физик и математик Симеон Дени Пуассон,1781-1840).

Процесс, про­исходящий без теплообмена с окружаю­щей средой, называется адиабатным, т. е. q = 0. Для того чтобы осуществить та­кой процесс, следует либо теплоизолиро­вать газ, т. е. поместить его в адиабат­ную оболочку, либо провести процесс на­столько быстро, чтобы изменение темпе­ратуры газа, обусловленное его тепло­обменом с окружающей средой, было пренебрежимо мало по сравнению с из­менением температуры, вызванным рас­ширением или сжатием газа. Как прави­ло, это возможно, ибо теплообмен про­исходит значительно медленнее, чем сжатие или расширение газа.

Параметры адиабатного процесса находятся путём решения дифференциального уравнения первого закона термоди­намики, которое для адиабатного процесса прини­мает вид:

c_v dT + pdv = 0.

Преобразовав и проинтегрировав, получаем

p₁ v₁ ^k = p₂ v₂ ^k.

Это и есть уравнения адиабаты идеального газа при постоянном отношении теплоемкостей (k = const).

Величина

k = c_p / c_v

называется показателем адиабаты. Согласно классической кинетической теории теплоемкость газов не зависит от температуры, поэтому можно считать, что величина k также не зависит от температуры и определяется числом степеней свободы мо­лекулы. Для одноатомного газа k = 1,66, для двухатомного k = 1,4, для трех- и многоатомных газов k =1,33.

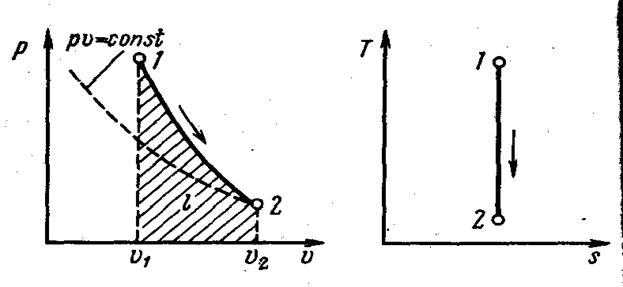
Рис. 4.4. Изображение адиабатного процесса в р, v- и Г, «-координатах

Поскольку k > 1, то в координатах р- v (рис. 4.4) линия адиабаты идет круче линии

 

изотермы, таким образом при адиабатном расши­рении давление понижается быстрее, чем при изотермическом, так как в процессе расширения уменьшается температура газа.

В адиабатном процессе Δq = с_ад = 0.