В одномерном случае общее решение уравнения (3) имеет вид

x = f₁ (x-υt) + f₂ (x +υt), (4)

где f₁ и f₂ — произвольные (дифференцируемые) функции. Первое слагаемое описывает распространение плоского сигнала f₁(x) со скоростью υ безизменения формы в направлении положительных х, а второе слагаемое — распространение сигнала f₂ (x) со скоростью υ внаправлении отрицательных х.

Пример 1. Упругий стержень.Силы, возникающие при продольных упругих деформациях стержня, подчиняются закону Гука: σ = Еε, где σ = F/S — напряжение в данной точке стержня (среды), e — (относительная) деформация D1/1, Е — модуль Юнга. Деформация в точке с координатой х выражается через частную производную: e=.

Сила, действующая на частицу среды размером Δх и массой Δm=рΔхS, равна σ(х + Δх) -σ(х). Уравнение движения частицы среды имеет вид:

Следовательно, скорость распространения волн в упругом стержне равна υ=.С такой же скоростью распространяется продольная волна в упругой среде.

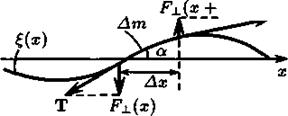
Пример 2. Натянутая струна. По струне, сила натяжения которой равна Т, может распространяться поперечная волна. Пусть профиль струны в данный момент задается функцией x(x,t) (рис.1). Получим уравнение движения частицы среды размером Dх в предположении «плавной» волны: дx/дх << 1. Вертикальная проекция силы натяжения равна F_^ (x)= Tsina » Т(дx/дх) (a — угол наклона струны); вертикальная сила,

действующая на частицу среды размером Dх и массой Dm = p₁DxS, равна F_^ (x + Dx) — F_^ (x) (p₁ —линейная плотность струны). Уравнение движения частицы среды имеет вид

'

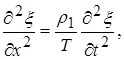следовательно, скорость распространения волн в струне равна υ=.

Пример 3. Воздушный столб в цилиндре. Объемная упругость газа (или любой термодинамически простой среды) характеризуется объемным модулем упругости К = —V(dp/dV) = r(др/дr). Значение К зависит от условий, при которых происходит объемная деформация газа. Для звуковых колебаний (n > 16 Гц) можно пренебречь теплообменом между разными частицами среды и считать К адиабатическим модулем упругости: K_ад = — V(dr/dV)_ад . Изменение давления в данной точке цилиндра равно (при малых деформациях) Dр(х) = —K(dV/V) = —К(дx/дх); сила, действующая на частицу воздушной среды размером Dх и массой Dm = r Dх S, равна DF = [Dр(х) — Dр(х + Dx)]S. Уравнение движения частицы среды имеет вид

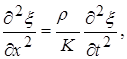
следовательно, скорость распространения волн в воздушном цилиндре равна υ== .(Эти выражения верны для любой термодинамически простой среды: для реального газа, для жидкости.) Для звуковых волн в идеальном газе получим: К = gр, u == , где g — показатель адиабаты .

Объемная плотность энергии. Плотность потока энергии.

Плотности кинетической и потенциальной энергии в данной точке плоской упругой продольной волны равны

.

Для бегущей волны произвольной формы x = f(x ± ut) выполняется соотношение (dx/dt)² =u²(dx/dx)². Учитывая, что для упругой продольной волны u² = Е/р, получим, что плотности кинетической и потенциальной энергии в каждой точке бегущей волны равны друг другу. Это утверждение верно для бегущей волны любой природы. В случае гармонической плоской волны (1) объемная энергия волны и ее среднее по времени значение имеют вид:

ω = ω_к + ω_п = ρ ω² sin²(ωt - kx), .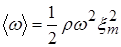

Плотность потока энергии (вектор Умова) в данной точке бегущей волны равна

U = ωu(5)

где u — скорость переноса энергии. Для бездисперсионной среды u = υ, где υ — скорость распространения волны, входящая в волновое уравнение (4). Для гармонической бегущей волны (1) и = υ, где υ — фазовая скорость волны: υ = ω/k. Энергия, переносимая бегущей волной через площадку ds за единицу времени (поток энергии), равна dФ = U·ds. Модуль среднего по времени значения модуля вектора Умова (его иногда называют интенсивностью волны) для гармонической плоской волны равен I = .В случае произвольной (в том числе стоячей) продольной упругой волны можно использовать выражение для U через мощность упругих сил (на единицу площади):

U=-σ

где σ = Е дξ,/дх — напряжение в данной точке среды (см. пример 1). Для поперечной волны в струне (пример 2) поток энергии имеет аналогичный вид:

P=T_^ =-.

Принцип суперпозиции волн.В линейной среде скорость волны не зависит от ее интенсивности, поэтому в такой среде выполняется принцип суперпозиции (наложения) волн:

результирующее возмущение в какой-либо точке линейной среды при одновременном распространении в ней нескольких волн равно сумме возмущений, соответствующих каждой из волн порознь.

Основываясь на принципе суперпозиции волн, можно заменить любую несинусоидальную волну в линейной среде эквивалентной ей системой синунусоидальных волн, т.е. представить в виде группы волн, или волнового пакета. Совокупность значений частот этих синунусоидальных волн называется спектром частот (или просто спектром) рассматриваемой несинусоидальной волны. В зависимости от характера колебаний, возбуждаемой волной, спектр частот последней может быть дискретным или непрерывным.

Дисперсия. Групповая скорость.Зависимость скорости гармонической волны от частоты или длины волны называется дисперсией, а среда, в которой наблюдается это явление, называется диспергирующей. В диспергирующей среде несинусоидальный бегущий импульс меняет свою форму в процессе движения, поскольку гармонические волны, входящие в его разложение Фурье, перемещаются с разной скоростью. Скорость переноса энергии, входящая в выражение (5) для вектора Умова, определяется в этом случае как скорость движения центра импульса (или как скорость точки, в которой деформация максимальна) и называется групповой скоростью волнового пакета (в отличие от фазовой скорости синусоидальной волны υ = w/k). Конечный импульс размером Δх называют волновым пакетом по той причине, что в его разложение в интеграл Фурье по гармоническим волнам входит конечная группа волн, спектральная ширина которой определяется соотношением: Δх·Δk ~ 1. Групповая скорость такого импульса равна

, (6)

где u = ω/k — фазовая скорость волны. Точки максимумов («горбы») внутри волнового пакета перемещаются с фазовой скоростью u, а огибающая этих максимумов — со скоростью u_гр (рис. 2).

Понятием групповой скорости волнового пакета можно пользоваться только в том случае, если его спектральная ширина столь мала, что зависимость ω(k) можно считать линейной.

Для иллюстрации рассмотрим волну, являющуюся суперпозицией всего двух бегущих волн близких частот и одинаковой амплитуды:

x = x_m cos[(w + Dw)t - (k + Dk)x] + x_m cos[w - Dw)t - (k - Dk)x] =

= 2x_m соз(Dw t — Dk x) cos(wt — kx).

Отсюда видно, что огибающая волн имеет пространственный период Dх =2π/Dk

и перемещается со скоростью и =Dw/Dk.

Пример 4.Групповая скорость может быть как меньше, так и больше фазовой. Фазовая скорость волн на поверхности жидкости для длинных (гравитационных) волн зависит от длины волны по закону υ=, а для коротких (капиллярных) волн — по закону υ=. Подставляя в формулу (6), находим, что групповая скорость в первом случае равна u_rp = υ/2, а во втором — u_гр = 3υ/2. Видно, что групповая скорость может сильно отличаться от фазовой.

Интерференция волн.Две волны называются когерентными, если в любой точке пространства они создают когерентные колебания, разность фаз которых не меняется со временем. Очевидно, что они имеют одинаковую частоту. Источники когерентных волн называются когерентными источниками. При сложении некогерентных волн средняя по времени энергия результирующего колебания равна сумме их средних энергий. При сложении когерентных волн, колебания частиц в которых происходят в одном или близких направлениях, может наблюдаться явление интерференции, т. е. устойчивое во времени ослабление колебаний в одних точках пространства и усиление — в других. Если точка находится на расстоянии r₁ от одного из когерентных источников и на расстоянии г₂ — от другого, то разность фаз между колебаниями в этой точке равна

Δφ=(φ₁₀ –kr₁) - (φ₂₀-kr₂)=2π.

Здесь Δφ_o- разность фаз между колебаниями источников, Δ— (г₂ — г₁) — разность хода волн. Условие максимума результирующих колебаний: Δφ=±2πт, условие минимума — Δφ=±2π(т+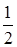), где т — порядок интерференционного максимума (минимума). В случае синфазных источников (Δφ₀ = 0) эти условия принимают особенно простой вид:

Δφ = ±тλ (максимум), Δφ = ±(т — 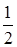)λ (минимум).

Пример 5.Рассмотрим два линейных когерентных источника цилиндрических волн, которые находятся на расстоянии λ/2 друг от друга. В точках, расположенных вдали от источников, разность хода волн определяется только направлением излучения и равна Δ =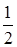λcos0 (рис. 3). В случае синфазных источников излу чение ослаблено в направлении θ = 0 и усилено в направлении θ = π/2, а в случае источников, совершающих колебания в противофазе (Δφ₀ = π), — наоборот.

Стоячие волны. Собственные колебания.Важным примером интерференции является стоячая волна, возникающая при сложении двух одинаковых плоских бегущих волн, распространяющихся навстречу друг другу:

x = x_mcos(ωt — kx) + x_mcos(ωt + kx) = 2x_mcoskx cos ωt (27)

Амплитуда колебаний точек волны А(х) = 2x_m cos kx периодически меняется от нуля (в узлах волны) до 2x_m (в пучностях волны). Расстояние между соседними узлами равно λ/2. Колебания точек между двумя узлами происходят в фазе, но по разные стороны узла — в противофазе. В узлах равна нулю амплитуда колебаний скорости, но максимальное значение имеет амплитуда колебаний деформации дx/дх. В пучностях, наоборот, отсутствуют деформации, но с максимальной амплитудой происходят колебания скорости. Средняя по времени энергия имеет одинаковое значение во всех точках стоячей волны. Вектор Умова равен нулю как в узлах, так и в пучностях, а в промежуточных точках периодически меняет свое направление.

Если конец стержня, совершающего колебательное движение, жестко закреплен, то смещение точек конца стержня равно нулю; если конец стержня свободен, то равна нулю деформация. В первом случае граничное условие имеет вид x| _х=о = 0, а во втором — дx/дх\_х=о =0, где значение х = 0 соответствует концу стержня. (Такие же условия возникают для колебаний воздуха в цилиндрической трубке в случае закрытого или открытого конца трубки. Для поперечных колебаний натянутой струны из примера 2 возможен только первый вариант, когдаконец струны закреплен.) Если все

 

Рис. 4

точки конечного стержня совершают гармонические колебания с одной частотой, то такое движение называют собственными колебаниями стержня. Если сделать мысленный разрез бесконечно длинного стержня в том месте, где находится узел стоячей волны, то будет удовлетворяться граничное условие для закрепленного конца, а если в том месте, где пучность, —то для свободного. Следовательно, свободные колебания стержня длиной l в случае двух свободных или двух закрепленных концов должны удовлетворять условию l = 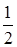mλ, ω_m=πmυ/l (спектр собственных колебаний, т = 1, 2, ...), а в случае одного закрепленного конца — условию l=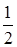(m -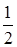λ) или ω_m=π (m-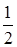)υ/l. Собственное колебание с наинизшей частотой называется основным колебанием, все остальные собственные колебания — обертонами или гармониками.

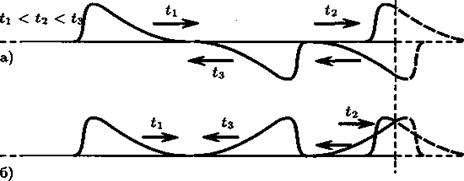
Отражение бегущей волны.Рассмотрим отражение бегущего импульса от конца стержня. Если конец стержня закреплен, то граничному условию ξ|_х=о = 0 и начальным условиям (один набегающий импульс) удовлетворяет суперпозиция набегающего импульса и точно такого же по форме бегущего ему навстречу импульса, в котором смещения точек имеют противоположное направление (рис. 5, а). Если же конец стержня свободен, то граничному условию дξ /дх|_х=о =0 удовлетворяет бегущий навстречу импульс смещений такого же знака (рис. 5, б). В случае бегущей волны отражение от свободного конца происходит без изменения фазы, при этом образуется стоячая волна с пучностью на конце стержня. Отражение от закрепленного конца происходит с изменением фазы на π, при этом образуется стоячая волна с узлом на конце стержня.

Эффект Доплера в акустике.При движении источника и (или) приемника волн относительно среды, в которой распространяется волна, регистрируемая частота отличается от излучаемой (если изменяется расстояние между источником и приемником). Направим ось х от приемника к источнику. Если источник излучает звук с частотой ν₀ и движется вдоль оси х со скоростью , то расстояние между соседними максимумами волны, распространяющейся вдоль х со скоростью v в направлении приемника, будет равно λ = υT₀ +T₀,а ее частота равна υ/λ:

v = v₀

Если приемник неподвижен, то он зарегистрирует именно эту частоту. Если приемник движется со скоростью , то интервал времени между приходом соседних максимумов равен Т' =λ (υ+ ), а частота принимаемого сигнала равна 1/Т':

v' = v₀

(29)

Эффект Доплера наблюдается в том случае, когда изменяется расстояние между источником и приемником.

 

Заключительная часть

 

Мы рассмотрели волновые движения в непрерывных средах. Такими непрерывными средами являются твердые тела или жидкости. Все эти объекты состоят из частиц, которые расположены близко к друг другу и для которых возможны небольшие смещения из положений их равновесия или мгновенных состояний. Причем взаимодействие частиц приводит к тому, что смещение части из них затрагивает соседние частицы. За счет этого и происходит передача энергии. Каждую такую частицу можно рассматривать как некий маленький маятник (осциллятор). А весь объект как совокупность осцилляторов. Если первоначально возбуждаются колебания небольшой группы таких осцилляторов, то в результате начинается распространение энергии в твердом теле или жидкости, т.е. совершается волновое движение. Далее, подробно будут рассмотрены свойства световых волн – дифракция и интерференция. Основным положением при рассмотрении волновых свойств является принцип Гюйгенса – Френеля.