Относительность длин и промежутков времени. Интервал между двумя событиями

1. Из преобразований Лоренца (1.5) следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения. Это изменение продольного размера тела при его движении называется лоренцевым сокращением.Пусть l₀ — длина стержня, покоящегося в системе отсчета К'. Если стержень расположен вдоль оси О'Х' (рис. 4), то l₀ = х'₂ — х'₁, где х'₂ и х'₁ — координаты концов стержня. Длина l того же стержня в системе отсчета К, относительно которой он движется вдоль оси ОХ со скоростью V, равна разности значений координат концов стержня, измеренных в один и тот же момент времени t:

 

l = x₂(t) – x₁(t) =( х'₂ — х'₁) √1 - V²/c² = l₀ √1 - V²/c² (1.12)

Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета:

y₂ — y₁ = y'₂ — y'₁ , z₂ — z₁ = z'₂ — z'₁ (1.12')

Итак, линейные размеры тела относительны. Они максимальны в той инерциальной системе отсчета, относительно которой тело покоится. Эти размеры тела называются его собственными размерами.

Лоренцево сокращение является кинематическим релятивистским эффектом. Оно не связано с действием на движущееся тело каких-либо продольных сил, сжимающих его

вдоль направления движения. Это сокращение заметно сказывается только при скоростях движения, близких к скорости света в вакууме. Из формулы для лоренцева сокращения следует, что тела не могут двигаться со скоростями V≥с, так как при V=с продольный размер тела становится равным нулю, а при V> с он должен был бы быть мнимым.

2. Еще одно важное следствие преобразований Лоренца — относительность промежутка времени между какими-либо двумя событиями (например, между началом и концом какого-нибудь процесса), т. с. зависимость этого промежутка времени от выбора инерциальной системы отсчета. Пусть в движущейся инерциальной системе отсчета К' два рассматриваемых события l и 2 происходят в одной и той же неподвижной относительно К' точке А (х'₂ = х'₁) в моменты времени t'₁ и t'₂, так что промежуток времени между этими событиями τ₀=t'₂ —t'₁. Относительно неподвижной инерциальной системы отсчета К точка А движется с той же скоростью V, что и система К'. Поэтому в К события 1 и 2 совершаются в разных точках с координатами х₁и х₂, причем х₂—х₁ == Vτ где τ = t₂ — t₁ — промежуток времени между событиями 1 2 по часам в системе отсчета К. Из преобразований Лоренца следует, что

(1.13)

Таким образом, промежуток времени между двумя событиями минимален в той инерциальной системе отсчета, относительно которой оба события совершаются в одной и той же точке. Время, измеряемое по часам, движущимся вместе с данным объектом, называется собственным временемэтого объекта. Рассмотренная нами закономерность свидетельствует о существовании релятивистского эффекта замедления хода времени:часы, движущиеся со скоростью V относительно данной инерциальной системы отсчета, идут медленнее в1/√l – V²/c²раз, чем неподвижные. Соответственно в согласии с принципом относительности все физические процессы в движущейся системе отсчета протекают медленнее, чем в неподвижной.

Эффект замедления хода времени становится заметным только при очень больших скоростях движения V, близких к скорости света в вакууме. Он подтверждается экспериментально, например, в опытах с мюонами. Мюон - нестабильная элементарная частица. Среднее собственное время жизни мюона (по часам в той инерциальной системе отсчета, относительно которой он покоится) τ₀ = 2,2 мкс. Мюоны рождаются в верхних слоях атмосферы под действием первичных космических лучей и движутся относительно Земли со скоростями К, близкими к с. Если бы релятивистского эффекта замедления хода времени не было, то по отношению к земному наблюдателю мюон мог бы пройти за время своей жизни путь к атмосфере, не превосходящий в среднем τ₀с = 660 м. Иными словами, мюоны не могли бы достигать поверхности Земли. В действительности они регистрируются приборами, установленными на поверхности Земли, так как среднее время жизни движущегося мюона по часам земного наблюдателя τ = (τ₀/√l – V²/c²)» τ₀ и путь, проходимый мюоном за это время, τV»660м.

3. Релятивистский эффект замедления хода времени в космическом корабле, движущемся относительно Земли, открывает возможность осуществления сколь угодно дальних космических полетов и путешествий «в будущее». Согласно принципу относительности, все процессы на космическом корабле, включая и процесс старения космонавтов, идут по тем же законам, что и на Земле. Однако при этом время на корабле нужно измерять по часам, движущимся вместе с ним со скоростью V относительно Земли. Если V близко к с, то часы на корабле идут значительно медленнее, чем на космодроме, а именно в 1/√l – V²/c² раз. Например, при β= V/c = 0,99999 ход часов на корабле и на Земле различается в 224 раза. Следовательно, на таком корабле за промежуток времени τ₀= 10 лет по корабельным часам можно совершить, постарев всего на 10 лет, космический перелет, который по часам на Земле будет продолжаться τ =2240 лет! При этом корабль удалится от Земли на огромное расстояние l= V τ = βc τ = 2239,98 св. лет (световым годомназывается расстояние, проходимое светом в вакууме за один год: 1 св. год = 9,46 • 10¹⁵ м). Чем ближе V к с, тем больший путь .' может пройти космический корабль относительно Земли за один и тот же промежуток to собственного времени на корабле, т. е. тем более дальний космический перелет могут совершить космонавты за свою жизнь. Если космонавт, совершив космический полет со скоростью V, близкой к с, возвратится на Землю, то он обнаружит, что люди на Земле (в частности, его брат-близнец, оставшийся на Земле) постарели за время полета больше, чем он. При достаточно малом отличии V от с, когда (1 — V²/c²)^-1/2» 1, космонавт может за время полета пережить всех своих сверстников на Земле и оказаться по возвращении на Землю среди представителей последующих поколений людей.

4. На первый взгляд кажется, что, основываясь на принципе относительности, можно прийти к прямо противоположным выводам: часы на Земле, движущейся со скоростью—V относительно космического корабля, должны отставать от часов на корабле. Поэтому длительность полета должна быть большей для космонавта, а не для жителей Земли. Соответственно за время полета должен сильнее постареть тот из двух близнецов, который летел на корабле. Таким образом, получается, что разность показаний часов на космодроме и на корабле после приземления последнего должна быть, с одной стороны, положительной, а с другой - отрицательной. Этот абсурдный результат получил название парадокса часов, или парадокса времени.В действительности никакого парадокса здесь нет. Он возник вследствие неправильного применения принципа относительности. Этот принцип говорит о полном равноправии не любых систем отсчета, а только инерциальных. Между тем система отсчета, связанная с космическим кораблем, в отличие от земной или, точнее, солнечной системы отсчета не все время является инерциальной, так как во время набора скорости после старта, при облете цели и торможении на участке спуска на Землю корабль движется с ускорением. Поэтому задача о ходе часов на космодроме, которые все время покоятся относительно одной и той же инерциальной системы отсчета, и часов на космическом корабле несимметрична, а соответствующие системы отсчета — неравноправны. Правильны рассуждения, изложенные вначале, поскольку они основаны на использовании инерциальной (земной) системы отсчета. Соответственно дальнейшие рассуждения, приведшие к парадоксу часов, ошибочны. Во втором случае нужно пользоваться не специальной, а общей теорией относительности. При этом оказывается, что и с точки зрения космонавта его часы должны идти медленнее, чем часы на космодроме.

 

 

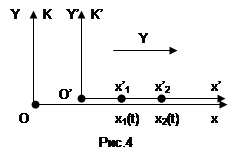Заключительная часть

 

Рассматривая выводы специальной теории относительности, видим что она, как, впрочем, и любые крупные открытия, потребовала пересмотра многих установившихся и ставших привычными представлений.

Основной вывод теории относительности сводится к тому, что пространство и время органически взаимосвязаны и образуют единую форму существования материи – пространство–время. Только поэтому пространственно-временной интервал между двумя событиями является абсолютным, в тот время как пространственные и временные промежутки между этими событиями относительны. Следовательно, вытекающие из преобразований Лоренца следствия являются выражением объективно существующих пространственно-временных соотношений движущейся материи.