Непрерывность функции на промежутке

 

Определение 1. Функция 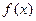называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка. Если концевая точка входит в промежуток, то непрерывность в ней понимаем как одностороннюю.

Дадим третье определение непрерывности в точке, которое будем использовать при доказательстве теоремы.

Допустим, что функция 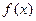определена в точке и некоторой ее окрестности. Рассмотрим точку из этой окрестности и приращение функции .

Определение 2. Функция называется непрерывной в точке , если она определена в этой точке и некоторой ее окрестности и

. (1)

Равенство (1) означает, что бесконечно малое изменение аргумента непрерывной функции влечет за собой бесконечно малое изменение самой функции.

Теорема 1. Всякая элементарная функция является непрерывной в области ее определения.

Доказательство. К элементарным функциям относятся: ; ; ; ; ; ; и др. тригонометрические функции; и др. обратные тригонометрические функции; ; ; и др. гиперболические функции. А также их линейные комбинации и сложные функции, образованные на их основе.

Докажем непрерывность функции для . Используем определение 2.

Рассмотрим

,

где произвольная фиксированная точка.

Тогда

,

т.к. (БМФ) и (ограниченная).

Аналогично для остальных функций.

 

Особое значение имеет непрерывность функции на отрезке. В этом случае можно доказать следующую теорему.

Теорема 2 (Вейерштрасса). Непрерывная на отрезке функция достигает на этом отрезке хотя бы один раз своего наибольшего и наименьшего значения.

Обозначают:

, .

Наибольшее значение функции – глобальный максимум, наименьшее значение функции – глобальный минимум.

С помощью понятия непрерывности функции можно определить также условия существования обратной функции.

Теорема 3.Если функция 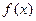определена, строго монотонна и непрерывна на некотором промежутке, то на этом промежутке существует для нее обратная функция, которая также является строго монотонной и непрерывной на своей области определения.