Понятие непрерывности функции в точке. Свойства непрерывных функций

Тема 2. Непрерывность функции

 

 

Определение. Функция 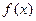непрерывна в точке , если она определена в этой точке и некоторой ее окрестности и если

. (1)

Понятие непрерывности функции в точке определено через понятие предела. Отличием от понятия предела является то, что требуется, чтобы функция была определена в самой точке. Кроме того, само значение предела при условии непрерывности должно совпадать со значением функции в точке. Поскольку в определении непрерывности используется предел, то основные свойства функций, имеющих предел, переносятся на непрерывность функции.

Свойства функций, непрерывных в точке:

1. Функция, непрерывная в точке, является ограниченной в некоторой окрестности этой точки.

2. Если функци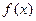и и 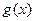непрерывны в некоторой точке , то непрерывными являются также функции:

;

;

;

, .

3. Если функция 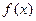непрерывна в точке и (), то существует некоторая окрестность точки , в которой ().

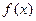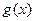4. Если и непрерывны в некоторой точке и , то существует некоторая окрестность точки , в которой .

5. Если функция непрерывна в точке , а функция непрерывна в точке , где , то сложная функция непрерывна в точке .

6. Если для сложной функции выполняются условия ее непрерывности (5), то справедлива формула

. (2)

Замечание 1. Свойства 3 и 4 означают, что некоторые особенности непрерывности функции в точке продолжаются на окрестность точки (продолжаются по непрерывности).

Замечание 2. Формула 2 означает, что для непрерывности функции в точке операции нахождения предела и функции переставимы (можно изменять их порядок). Этим пользуются при вычислении пределов.

 

Например: .