Импульс механической системы. Закон сохранения импульса замкнутой системы

Рассмотрим систему материальных точек. Импульс системы равен геометрической сумме импульсов всех n материальных точек системы:

.

Преобразуя последнее равенство и используя формулу (2.11), получим:

. (2.14)

Из (2.14) следует, что импульс системы точек равен произведению массы всей системы на скорость ее центра масс.

Преобразовав уравнение (2.13) с учетом выражения (2.14), получим,

. (2.15)

Уравнение (2.16) выражает теорему об изменении импульса системы: скорость изменения импульса механической системы равна сумме всех внешних сил, приложенных к системе.Согласно уравнению (2.15), импульс системы может изменяться под действием только внешних сил. Внутрен­ние силы не могут изменить импульс системы.

Замкнутой системой называют систему точек, на которую не действуют внешние силы. Для замкнутой системы правая часть уравнения (2-15) равна нулю:

или .

Полученное равенство выражает собой закон сохранения импульса: импульс замкнутой системы не изменяется со временем. При этом импульсы отдельных точек или частей замкну­той системы могут меняться со временем:

,.

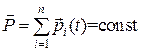однако эти изменения всег­да происходят так, что приращение импульса одной час­ти системы равно убыли импульса оставшейся части системы.

1. Импульс может сохра­няться и для незамкнутой сис­темы при условии, что ре­зультирующая всех внешних сил равна нулю.

2. У незамкнутой системы может сохраняться не сам импульс , а его проекция P_х на некоторое направле­ние х. Причина этого заключается в том, что когда проекция результирующей внешней силы на направление х равна нулю, т. е. вектор перпендикулярен ему. Действительно, спрое­ктировав уравнение (2.16),получим

,

откуда следует, что если 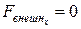, то P_x=const. Напри­мер, при движении системы в однородном поле сил тя­жести сохраняется проекция ее импульса на любое гори­зонтальное направление независимо от процессов, происходящих в системе. При горизонтальном перемещении человека в первоначально покоящейся лодке, импульс системы человек-лодка лодка будет равен нулю. Центр масс системы человек-лодка будет неподвижен, так как сумма внешних сил в горизонтальном направлении равна нулю (если пренебречь силами сопротивления) и согласно (2.14) скорость центра масс также равна нулю.

Пример 2.1. Найти закон движения материальной точки, движущейся по прямой под действием упругой силы F = –kx. Движение начинается из начала координат x=0 в момент времени t = 0 с начальной скоростью υ₀.

Уравнение (2.3) в одномерном случае () примет вид:

. (2.17)

Это дифференциальное уравнение с постоянными коэффициентами. Из математики известно, что решение этого дифференциального уравнения имеет вид:

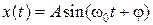. (2.18)

Константы A и φ найдем из начальных условий:

.

Значение ω₀ определим, подставив решение (2.18) в уравнение (2.17):

.

Искомый закон имеет вид:

.

 

Движение, которое задано синусоидальной функцией (2.18), называется гармоническим колебанием. Величина w₀ есть циклическая частота собственных колебаний материальной точки, А – амплитуда колебаний, φ - начальная фаза.

Пример 2.2. Применение закона движения центра масс для расчета сил трения скольжения.

Однородный цилиндр массой m равномерно вращается между двумя взаимно перпендикулярными плоскостями (рис. 2.3). Коэффициент трения скольжения цилиндра о плоскости равен m. Найти силы трения скольжения.

На цилиндр действуют силы трения 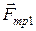и , силы реакции со стороны плоскосте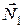й,и и сила тяжести mg (рис. 2.3), которые являются внешними, т. е. обусловлены действием внешних тел. Центр масс цилиндра (точка, которая лежит на оси цилиндра С) неподвижен. Поэтому левая часть уравнения (2.14) равна нулю. Перепишем это уравнение в проекциях на оси x и y:

 

(2.19)

Силы трения скольжения равны F_тр1 = mN₁ и F_тр2 = mN₂ . Подставив эти выражения в (2.19), получим:

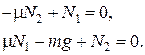
Рис. 2.3

 

Умножим второе уравнение в (2.19) на μ и сложим с первым:

.

Отсюда найдем силу N₁ :

.

Сила трения F_тр1 равна:

.

Из первого уравнения в (2.19) выразим силу N₂= N₁/m и найдем силу трения F_тр2:

.