На разветвляющиеся алгоритмы.
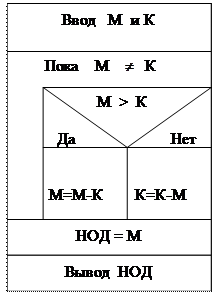
1. Пусть надо определить наибольший общий делитель двух целых чисел М и К
2. Поиск максимального или минимальногоиз трех и более значений.
Пусть надо найти МАХ –е из трех чисел А, В и С.
Результат запишем в переменную с именем МАХ.
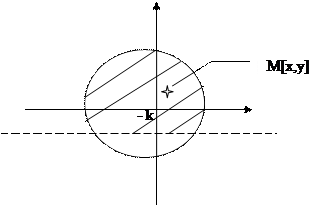
3. Составить алгоритм попадания точкиМ с координатами х и у M[x,y] в заштрихованную область. x2 + y2 =R2 - уравнение окружности с центром в начале координат.
У
Условие попадания в заштрихованную
Х область состоит из двух частей:
x<=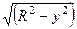
y>= -k
Алгоритм:
1. Ввести R
2. Ввести координаты точки х и у
3. ЕСЛИ x<=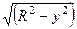 и одновременно y >= -k, ТО печатать сообщение «Точка M[x,y] попала в заштрихованную область» ИНАЧЕ печатать сообщение «Точка M[x,y] НЕ попала в заштрихованную область»
4. Конец.
4. Составление алгоритма вычисления функции f(x) при произвольном значении аргумента x:
, если x < -5;
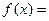
, если -5 
-1;
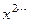+2 , если -1 < 
;
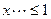в остальных случаях функция не определена.
1. Анализ задания: исходное значение Х может быть любым. Результат – F.
2. Блок-схема.
F1 F – не определена
 |
-5 -1 1 x
5. Составление алгоритма вычисления функции f(x) при любом х, представленной графиком:
1. Анализ задания. Имеем 5 участков с разными функциями.
Представим график в аналитическом виде:
Y
1
-1 0 1 2 X
уравнение прямой имеет вид y= kx + b. В нашем случае при х=0
y= -x – 1
Уравнение окружности с центром в начале координат [0;0] и с радиусом R имеет вид: x2 + y2 = 1 . При этом y = 
.
Уравнение окружности со смещенным вправо на единицу центром [1;0] и с радиусом = 1 имеет вид:
(x-1)2 + y2 = 1 y = 
.
На основании вышеизложенного запишем аналитический вид графика функции:
, если x < -1;
, если -1 < x <= 0;
Y(x) = 1 , если 0 < x <= 1
, если 1 < x <= 2;
0 , если x>2.
Алгоритм в виде структурограммы:
 |
X
 |
КонеыК