Составное высказывание, образованное в результате ДИЗЪЮНКЦИИ, истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Составное высказывание, образованное в результате КОНЪЮНКЦИИ, истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.
Логические функции двух переменных.
Для кодирования одного символа необходим 1 байт информации.
Лекция 3. 4. Логические основы ЭВМ.
Логика – ЭТО НАУКА О ФОРМАХ И СПОСОБАХ МЫШЛЕНИЯ.
Основными формами мышления являются: понятие, высказывание и умозаключение.
ПОНЯТИЕ – фиксирует основные, существенные признаки объекта.
ВЫСКАЗЫВАНИЕ – это форма мышления, в котором что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть ИСТИННО или ЛОЖНО.
УМОЗАКЛЮЧЕНИЕ – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).
Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда, если умозаключение проводится в соответствии с правилами формальной логики, то оно будет истинным. В противном случае можно прийти к ложному умозаключению.
Для того, чтобы можно было определить истинность или ложность высказываний, не вникая в их содержание, была придумана алгебра высказываний. В этой алгебре высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «истина» (1) и «ложь» (0). В этой алгебре можно производить некоторые логические операции над высказываниями, получая в результате новые составные высказывания .
Существует раздел математики- БУЛЕВА АЛГЕБРА, изучающая логические операции над логическими(«двоичными») переменными. По аналогии с классическими числами над этими переменными могут осуществляться различные операции с использованием логических функций.
2
Имеется 22=16 функций (2- переменные, 2- состояния 0 или 1).
Функции эти называются КОНСТИТУАНТЫ нуля и единицы.
Базовые логические операции И, ИЛИ, НЕ.
ИОбъединение двух высказываний в одно с помощью союза «И» называется операцией логического умножения или конъюнкцией.
| А | В | F= A & B |
На формальном языке алгебры логики операция конъюнкции обозначается значком «&» или «^ ». Например, F= A & B. Аргументы могут принимать значения 1 или 0 и результат тоже только значения 1 или 0. Значение логической функции F можно определить из таблицы истинности этой функции.
ИЛИОбъединение двух высказываний в одно с помощью союза «ИЛИ» называется операцией логического сложения или дизъюнкцией.
| А | В | F= A + B |
На формальном языке алгебры логики операция дизъюнкции обозначается значком «+» или «\/ ». Например, F= A + B. Аргументы могут принимать значения 1 или 0 и результат тоже только значения 1 или 0. Значение логической функции F можно определить из таблицы истинности этой функции.
Функция «ИСКЛЮЧАЮЩЕЕ ИЛИ» 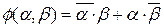
 , если
, если  или
или 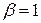 , но не одновременно. Еще ее называют «Сумма по модулю 2» или «Функция несовпадения» , обозначается
, но не одновременно. Еще ее называют «Сумма по модулю 2» или «Функция несовпадения» , обозначается 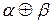 .
.
НЕПрисоединение частицы «не» к высказыванию называется операцией логического отрицанияилиинверсией. Инверсия делает истинное высказывание ложным и наоборот, ложное - истинным.На формальном языке отрицание обозначают чертой над аргументом.
Логические выражения. (Дать пример составления логического выражения и по нему – таблицы истинности).
 №
набора
Перем. №
набора
Перем.
| ||||

| ||||

| ||||
| с |
Например, надо вычислить значение логического выражения при заданном наборе исходных переменных:
_______________
(
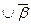 )
)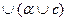
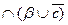 , где
, где
(Дать решения для каждого из наборов и на следующей лекции – контрольная работа по таким задачам – на один час.)
Кроме базовых функций, которые мы рассмотрели (И. ИЛИ и НЕ) существуют еще 13 функций от двух аргументов, которые построены на базовых. Рассмотрим две самые часто используемые: ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ (ИМПЛИКАЦИЯ) и ЛОГИЧЕСКОЕ РАВЕНСТВО ( ЭКВИВАЛЕНТНОСТЬ).
СЛЕДОВАНИЕ (ИМПЛИКАЦИЯ) обозначается стрелкой → «если А, то Б»
| А | В | F= A → B |
Составное высказывание, образованной с помощью ИМПЛИКАЦИИ (следования) , ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание). Докажем методом сравнения таблиц истинности , что операция ИМПЛИКАЦИИ равносильна логическому выражению НЕ А ИЛИ В, т.е. построены на базовых логических функциях:
| А | В | ⌐ А | ⌐ А \/ В |
РАВЕНСТВО ( ЭКВИВАЛЕНТНОСТЬ) обозначается волнистой чертой ~ «А тогда и только тогда, когда В»
Составное высказывание, образованной с помощью эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны , либо истинны.
| А | В | F= A ~ B |
Рассмотрим законы и теоремы алгебры логики (или Булевой алгебры):
1. 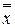 = х
= х
2. х + у = у + х
3. х * у = у * х
4. х + у + а = (х+у) + а = х + (у+а)
5. хуа = (ху)а = х(уа)
6. х(у+а) = ху+ха
7. х + уа = (х+у) (х+а)
8. х +х = х
9. х*х = х
10. х + 0 = х
11. х * 1 = х
12. х *0 = 0
13. х + 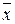 =1
=1
15. х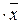 =0
=0
16. х + ху = х
17. х(х+у) + х
18. х + 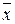 у = х + у
у = х + у
19. х(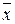 + у) = ху
+ у) = ху
20.  =
= 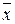 *
*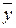 *
*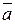 …
…
21.  =
= 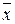 +
+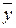 +
+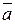 …
…
Последние два пункта - общие случаи теоремы Де Моргана, которая звучит так: «Отрицание логической суммы равно логическому произведению отрицаний и отрицание логического произведения равно логической сумме отрицаний.»
Упрощение логических выражений с использованием теорем:
Обычно начинают с поиска следующих форм:
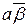 +
+
 +
+
 +
+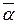
 , где
, где  и
и  либо сами логические переменные, либо произведения множеств логических переменных.
либо сами логические переменные, либо произведения множеств логических переменных.
Эти структуры можно упростить:
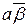 +
+ =
= (
( +
+ )=
)=
 +
+ =
= (1+
(1+ )=
)=
 +
+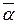
 =(
=( +
+ )+
)+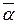
 =
= +(
+(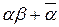
 )=
)=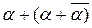
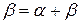
Например:  *у*
*у*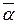 +
+ 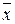 *
* 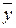 *
*  + х *
+ х * 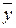 *
*  +
+ 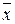 *у * а + х*у*
*у * а + х*у* =
=
---------------- =========== ---------------- ========
сгруппируем 1-й и 4-й , 3-й и 5-й и получим:
= 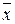 *у*(
*у*(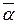 +
+ )+
)+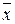 *
*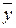 *
* +х
+х (
(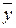 +у)=
+у)= 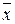 у+
у+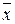
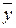
 +х
+х =
=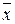 (у+
(у+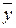
 )+х
)+х =
=
=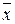 (у+
(у+ )+х
)+х =
=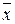 у+
у+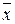
 +х
+х =
=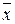 у+
у+ (
(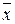 +х)=
+х)= 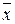 у+
у+
Вычислительные процессы в ЭВМ решаются с помощью правильно построенных логических схем, где на входе может быть несколько сигналов высокого (1) и низкого (0) уровня. Чтобы эти схемы упростить, минимизировать затраты и экономические и временные, все первоначальные логические выражения упрощаются, используя выше описанные тождества и законы Булевой алгебры.
Например; Дана схема с четырьмя аргументами – сигналами и выход S = инверсия функции F(a,b,c,d).

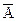
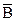
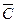

Запишем функцию : 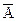
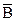
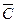
 +
+ 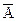 В
В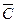
 +
+ 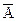
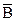 С
С +
+ 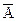 ВС
ВС =
=
объединим 1 и 3й, 2 и 4-й:
=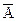
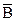
 (
(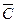 +С) +
+С) + 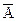 В
В (
(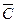 + С) =
+ С) = 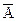
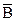
 +
+ 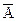 В
В =
= 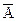
 (
(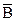 +В) =
+В) = 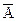

F(a,b,c,d)= 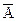
 =
= 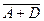
Инверсия этого выражения -  = А +D, т.е. схема сводится к виду:
= А +D, т.е. схема сводится к виду:
| |
А


 D
D
Упрощение логических выражений с использованием теорем:
Обычно начинают с поиска следующих форм:
А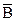 + АВ или А + АВ или А +
+ АВ или А + АВ или А + 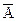 В , где А и В логические переменные. Эти структуры можно упростить:
В , где А и В логические переменные. Эти структуры можно упростить:
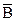 + АВ = А(
+ АВ = А(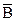 +В) = А
+В) = А
А + АВ = А(1 + В) = А
А + 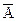 В = (А + АВ) +
В = (А + АВ) + 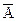 В = А + (АВ +
В = А + (АВ + 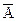 В) = А + (А +
В) = А + (А + 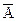 )В = А + В
)В = А + В
Бывает необходимость упрощения схемы в обратном порядке, то есть предлагается готовая логическая схема, которую необходимо упростить. для этого по схеме записываются цепочки логических выражений, которые в свою очередь упрощаются уже рассмотренными методами. Значит надо уметь записывать логические выражения по предложенным схемам. НАПРИМЕР.




|
|

|


 у не х
у не х





|
|

 у х
у х
_________________________ ____________ _________ ________ __ _
_ _
( ( х * у ) + х ) + ( ( х + у ) * х ) = у + х +х + х*у = у +1 + х*у = у(х+1) +1=у+1=1 = 0.
Получается при упрощении выражения, что при любых входных сигналах на выходе будет НОЛЬ, то есть эта схема может служить как генератор нуля.
Лекция № 4 5. Основные этапы развития вычислительной техники.
(К вопросу об истории вычислительной техники)
(Раздать таблицу с поколениями ЭВМ)!!!!!!
Цифровая ВТ развивается многие тысячелетия. Началось все со счетных камешков, палочек; около 2000 лет назад, в так называемый «механический век», появились АБАКи (счеты), которые сохранились до сих пор.
Идея создания счетной машины долго витала в воздухе, были попытки создания не доведенные до конца, и только в 1936 году английский математик АЛАН ТЬЮРИНГ доказал возможность построения универсального вычислительного устройства (машина ТЬЮРИНГА). В 1946 году ДЖОН ФОН НЕЙМАН предложил ряд новых идей организации ЭВМ, в том числе – хранить программы в запоминающем устройстве. В результате была создана архитектура ЭВМ, во многом сохранившаяся до настоящего времени.
В СССР работы по созданию универсальной ЭВМ начались под руководством академика Лебедева С.П. в конце 30-х годов, но в 1941 году были прерваны. И только в 1948-50гг была создана МЭСМ, а в 1953 г – БЭСМ, выполняющая 10000 операций в сек. и бывшая в то время лучшей в мире.
С момента создания первых ЭВМ прошло 5 поколений их развития:
| Поко- ление | Годы вы- пуска пер- вых ЭВМ | Макс. быстро- действ. | Элементная база | Ср-во сваязи с пользователем. | Язык программирования | Мировой парк ЭВМ |
| 1953-54 | 103 - 104 | Электронная лампа | Пульт управления и перфокарты | Машинный код | (1960г) | |
| 1958-60 | 104 – 106 | Транзистор | Перфокарты | Ассемблер | 30тыс (1965г) | |
| 1965-66 | 105 – 107 | Малая интегральная схема(ИС-2) 5тр. | Алфавитно-цифровой терминал | Ассемблер, процедурные языки высокого уровня | 300тыс (к 1975г) | |
| 1976-79 | 106 – 108 | БИС (10000тр) | Цветной графический дисплей | Процедурные языки высокого уровня | 1,2 млн (1980) | |
| 1990-92 | 108 – 1012 | СБИС (106 тр) | Устройство голосовой связи | Непроцедурные языки высокого уровня | 150 млн. (1990) |
У машин 5-го поколения архитектура существенно отличается от предыдущих.
В настоящее время ведутся работы по созданию нейрокомпьютеров и даже биокомпьютеров, имеющих совершенно другую архитектуру.