Система сходящихся сил
Плоской системы сил
Система сходящихся сил. Условия равновесия
Лекция 2.
Системой сходящихся сил (или пучком сил) называется такая система сил, линии действия которой пересекаются в одной точке – центре пучка.
Равнодействующая системы сходящихся сил равна векторной сумме слагаемых сил и определяется замыкающей стороной силового многоугольника, построенного на слагаемых силах как на составляющих. Точка приложения равнодействующей силы совпадает с точкой пересечения линий действия сил.

Проекции равнодействующей силы на оси координат равны алгебраической сумме проекций составляющих сил на эти оси.

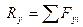


Рис. 2.1
Условия равновесия системы сходящихся сил в векторной форме
Для равновесия сходящейся системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая сила была равна нулю.

Условия равновесия системы сходящихся сил в алгебраической форме
Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех прямоугольных осей координат были равны нулю.


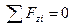
Пример 2.1. Груз весом Q равномерно поднимается тросом лебедки, перекинутым через неподвижный блок, который подвешен на двух шарнирно закрепленных стержнях. Пренебрегая размерами блока, трением и весом каната, определить усилия Т1 и Т2 в стержнях (рис. 2.2. а).

Рис. 2.2
Применяя аксиому об освобождаемости от связей и считая, что натяжение каната на участке между лебедкой и блоком равно весу Q груза, составим расчетную схему (рис.2.2.б).
Учитывая условия равновесия для плоской системы сходящихся сил, запишем:
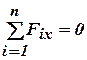 ;
; 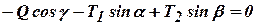 ;
;
 ;
;  .
.
Как видно, получена система двух линейных уравнений с двумя неиз-вестными, решая которую определяем усилия Т1 и Т2 в стержнях.
Если в результате решения получается отрицательная реакция связи, то необходимо старое направление этой реакции заменить на противоположное, отбросив минус.
Для проверки правильности решения необходимо полученные значения реакций Т1 и Т2 подставить в систему уравнений и убедиться в их тождестве.