Критерии Михайлова

Критерий Михайлова относится к группе частотных критериев устойчивости. Он был сформулирован и обоснован в 1936 г. совет­ским ученым А. В. Михайловым в работе «Гармонический метод в теории регулирования», которая получила высокую оценку и по­служила началом широкого применения частотных методов в тео­рии автоматического управления.

Критерий Михайлова так же, как критерии Гурвица и Рауса, основан на анализе характеристического уравнения системы, поэ­тому с его помощью можно судить об устойчивости замкнутых и разомкнутых систем.

Пусть левая часть характеристического уравнения, называе­мая характеристическим полиномом, имеет вид

F(p) = a₀ pⁿ+ a_n-1 p^n-1+…+ a _n-1 p+ a_n. (4.11)

Подставим в этот полином вместо переменного р чисто мнимый корень, который в дальнейшем будем обозначать jw. Тогда получим функцию комплексного переменного

F(jw) = a₀ (jw)ⁿ+ a_n-1 (jw)^n-1+…+ a _n-1 jw+ a_n, (4.12)

которую можно так же, как амплитудно-фазовую характеристику, представить в виде суммы действительной и мнимой частей:

F(jw) = P(w) + jQ(w). (4.13)

Действительная часть P(w) содержит только четные степени переменного w:

P(w) = a_n - a _{n - 2}w² + a _{n - 4}w⁴ - . . . , (4.14)

а мнимая часть Q(w)— только нечетные:

Q(w) = a_n-1w - a _{n - 3}w³ + a _{n - 5}w⁵ - . . . . (4.15)

Каждому фиксированному значению переменного w соответст­вует комплексное число, которое можно изобразить в виде вектора на комплексной плоскости. Если теперь изменять параметр w от 0 до ¥, то конец вектора F(jw) опишет некоторую линию (рис. 4.2, a), которая называется характеристической кривой или годографом Михайлова. По виду этой кривой можно судить об устойчивости системы.

Формулировка критерия Михайлова:

автоматическая система управления, описываемая уравнением п-го порядка, устойчива, если при изменении w от 0 до ¥ характеристический вектор системы F(jw) повернется против часовой стрелки на угол п p/2, не обращаясь при этом в нуль.

Это означает, что характеристическая кривая устойчивой си­стемы должна при изменении w от 0 до ¥ пройти последовательно через п квадрантов. Из выражений (4.14) и (4.15) следует, что кри­вая F (jw) всегда начинается в точке на действительной оси, уда­ленной от начала координат на величину а_n.

Характеристические кривые, соответствующие устойчивым си­стемам (рис. 4.2, б), имеют плавную спиралеобразную форму и ухо­дят в бесконечность в том квадранте, номер которого равен порядку уравнения. Если характеристическая кривая проходит п квадран­тов не последовательно или проходит меньшее число квадрантов, то система неустойчива (рис. 4.2, в).

 

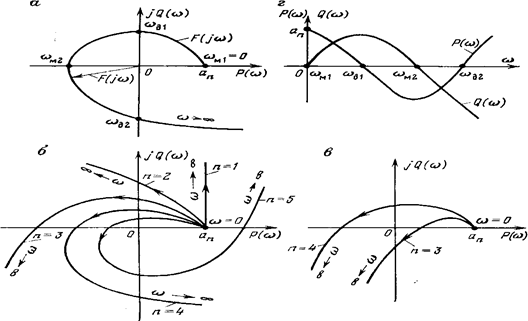
Рис. 4.2. Характеристические кривые (годографы) Михайлова

 

Если кривая F(jw) проходит через начало координат, то си­стема находится на границе устойчивости. Действительно, если характеристическое уравнение имеет один нулевой корень p_k = 0 (апериодическая граница устойчивости) или одну пару чисто мнимых корней p_k = ± jb_k (колебательная граница устойчивости), то функция F(jw) при w = 0 или w = b_k обратится в нуль.

В практических расчетах удобно применять следствие из критерия Михайлова: система устойчива, если действительная и мнимая части ха­рактеристической функции F(jw) обращаются в нуль пооче­редно (рис. 8.2, г), т. е. если корни уравнений P(w) = 0 и Q(w) = 0 перемежаются.

Это утверждение вытекает непосредственно из формулировки критерия Михайлова — из условия последовательного прохожде­ния кривой F(jw) через п квадрантов.

Критерий Михайлова удобно применять для анализа устойчи­вости систем высокого порядка (п > 5).