Дифференциальное исчисление функции
К У Р С
О рекомендации к изданию конспекта лекций по курсу «Паліталогія».
Разное.
Слушали:
Заведующего кафедрой гуманитарных дисциплин Бубнова Ю.М., который доложил, что на кафедре ГД подготовлен к изданию конспект лекций объёмом 11 п.л. по курсу «Паліталогія», авторы – Бубнов Ю.М., Пушкин И.А.
Постановили:
Рекомендовать к изданию конспект лекций по курсу «Паліталогія», авторы – Бубнов Ю.М., Пушкин И.А.
Председатель Носиков А.С.
Секретарь Андреева И.И.
Министерство образования Республики Беларусь
УО «Могилевский государственный университет продовольствия»
ВЫПИСКА ИЗ ПРОТОКОЛА
05.04.06 г. г. Могилев № 7
заседание кафедры
гуманитарных дисциплин
Председатель - Бубнов Ю.М.
Секретарь – Синявская И.Л.
Присутствовали: Бубнов Ю.М., Бобкова Т.Г., Воронова Е.Н., Жуков В.З., Кармазинов Л.С., Костеров А.П., Михальчук Н.Е., Пушкин И.А., Соклакова Н.В., Таборко Н.Г., Юдин В.В., Синявская И.Л., Бочкова С.В., Еселевская В.Г., Демидова Н.Л., Аленькова Ю.В., Рожковский В.Л.
Повестка дня:
1. О рекомендации к изданию конспекта лекций по курсу «Паліталогія», авторы: доктор социологических наук Бубнов Ю.М., кандидат исторических наук Пушкин И.А.
Постановили:
1. Рекомендовать к изданию конспект лекций по курсу «Паліталогія» , авторы: доктор социологических наук Бубнов Ю.М., кандидат исторических наук Пушкин И.А.
Голосовали единогласно
Председатель,
заг.кафедры, д.с.н. Ю.М.Бубнов
Секретарь И.Л.Синявская
[1] К.Г.Юнг Очерки о современных событиях. Психология нацизма. // Цит. по: Одайник В. Психология политики. Политические и социальные идеи Карла Густава Юнга. Изд. «Ювента»: 1996. – С. 272.
[2] Ришар Ж.-Ф. На переломе: Двадцать глобальных проблем – двадцать лет на их решение / Пер. с англ.. В.Ф.Мисюченко. - М.: Ладомир, 2006. – 240 с. – С. 32.
[3] Кропоткин П.А. Взаимная помощь как фактор эволюции. – М., 1918. – 214 с. – С. 214.
[4] Бакунин М.А. Избр. филос. соч. и письма. – М., 1987. С. 226.
В Ы С Ш Е Й
М А Т Е М А Т И К И
Краткий конспект лекций
ЧАСТЬ 2
одной переменной.
Производная функции, ее геометрический и физический смысл.
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
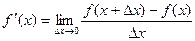
 у
у
f(x)
f(x0 +Dx) P
Df
f(x0) M
a b Dx
0 x0 x0 + Dx x
Пусть f(x) определена на некотором промежутке (a, b). Тогда  тангенс угла наклона секущей МР к графику функции.
тангенс угла наклона секущей МР к графику функции.

 ,
,
где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой: 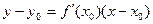

Уравнение нормали к кривой:  .
.
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.
Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.
Односторонние производные функции в точке.
Определение. Правой (левой) производной функции f(x) в точке х = х0 называется правое (левое) значение предела отношения  при условии, что это отношение существует.
при условии, что это отношение существует.

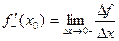
Если функция f(x) имеет производную в некоторой точке х = х0, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х0, а во- вторых, даже если функция непрерывна в точке х0, она может быть в ней не дифференцируема.
Например: f(x) = ïxï- имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.
Теорема. (Необходимое условие существования производной) Если функция f(x) имеет производную в точке х0, то она непрерывна в этой точке.
Понятно, что это условие не является достаточным.
Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (u ± v)¢ = u¢ ± v¢
2) (u×v)¢ = u×v¢ + u¢×v
3)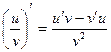 , если v ¹ 0
, если v ¹ 0
Эти правила могут быть легко доказаны на основе теорем о пределах.
Производные основных элементарных функций.
1)С¢ = 0; 9) 
2)(xm)¢ = mxm-1; 10) 
3)  11)
11) 
4)  12)
12) 
5)  13)
13) 
6)  14)
14) 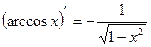
7)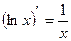 15)
15) 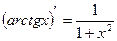
8)  16)
16) 
Производная сложной функции.
Теорема.Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Тогда 