Решение обыкновенных дифференциальных уравнений. Метод Эйлера

КОБЕЦ Е.В.

ЛЕКЦИОННЫЙ МАТЕРИАЛ

ПО ДИСЦИПЛИНЕ «КОМПЬЮТЕРНОЕ

ОБЕСПЕЧЕНИЕ»

Решение обыкновенных дифференциальных уравнений. Метод Эйлера

Обыкновенные дифференциальные уравнения встречаются достаточно часто в различных прикладных задачах. Ими описываются задачи движения систем материальных точек, электрических цепей и др.

Определения:

Дифференциальным называется такое уравнение, которое связывает независимую переменную Х, ее функцию y=f(x) и производные этой функции .

В неявном виде дифференциальное уравнение записывается так:

F(x, y, )=0.

Порядок старшей производной, входящей в это уравнение, называется порядком дифференциального уравнения.

Если y=f(x) – функция одного независимого переменного Х, дифференциальное уравнение называется обыкновенным, если же y=f(x₁,x₂,…x_n) – функция n независимых переменных x₁,x₂,…x_n, то уравнение называется уравнением в частных производных.

Решение обыкновенного дифференциального уравнения сводится к поиску функции y=f(x), которая при подстановке в уравнение обращает его в тождество.

Поиск решения такого уравнения называется его интегрированием, а полученное решение – интегралом этого уравнения.

Существуют общее и частное решения дифференциального уравнения.

Общим решением уравнения является функция y=φ(x,c), удовлетворяющая уравнению при любых значениях постоянного С.

Частное решение определяется конкретным значением С. Для нахождения частного решения необходимо указать начальные условия, т.е. задать значения y, при х=х₀, т.е. y₀=y(x₀), …,

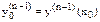
Задача отыскания решения обыкновенного дифференциального уравнения при начальных условиях называется задачей Коши для обыкновенного дифференциального уравнения.

Мы рассматриваем уравнения разрешенными относительно старшей производной.

Их можно свести к системе n обыкновенных дифференциальных уравнений первого порядка заменой 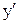на неизвестную функцию Р₁(х), на Р₂(х) и т.д., т.е.

1 производная 2 производная

Исходное уравнение в новом виде

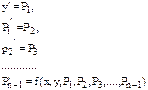
Причем, начальные условия:

Для решения мы будем рассматривать методы Эйлера и Рунге-Кутта.

Численное решение состоит в построении таблицы приближенных значений y₁,y₂,…,y_n_-1 точного решения y(x) уравнения .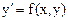

Мы не знаем вида функции, не можем сразу вычислить значение функции. Знаем только начальные условия, значения Х₀=а, y₀=y(x₀) и интервал [a,b], на котором необходимо проинтегрировать функцию.

Задача ставится так: в точках Х₀,X₁,…,Х_n нужно найти приближения y₀,y₁,…,y_n точного решения.

Первый шаг – разбиваем отрезок на конечное число узловых точек (узлы сетки). Шаг сетки h=(b-a)/n, X_i=a+ih, I=0,1,..,N.

Нужно восстановить значения искомой функции. Рассмотрим дифференциальное уравнение 1 порядка

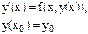
Второй шаг – зная начальные условия вычисляем значение первой производной в точке Х₀.

Третий шаг – в следующем узле сетки вычисляем значение функции.

На четвертом шаге все повторяется.

Геометрическая интерпритация метода состоит в замене интегральной кривой на отрезке касательной к ней в точке x_i,y_i. На каждом шаге заново определяется касательная, и, следовательно, соответствующая приближенному решению кривая будет ломаной линией. Поэтому метод называют еще методом ломаных.

Схема вычислений: x_i=a+ih (I=0,1,…,N)

Т.е. имея известную точку, вычисляем следующую. Это схема вычислений для уравнения 1 порядка.

Метод Эйлера для уравнений 2 порядка надо уравнение с начальными условиями 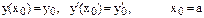свести к системе 2 уравнений 1-го порядка:

Производные берутся в точке х.

Итерационная формула вычислений:

На практике вычисления проводятся снизу вверх: вначале вычисляется 1 производную, т.е. p_i, а затем вторую Y_i_.

Для уравнения второго порядка приходится дважды применять интегрирование. Восстанавливаем значение производной, а затем значение искомой функции, т.е. решаем вначале одно уравнение, а затем второе.

Пример. На отрезке [a,b] составить таблицу значений приближенного решения дифференциального уравнения , удовлетворяющего начальным условиям

Y(0)=1, Y΄(0)=2. шаг интегрирования h=0,2, точность ε=0,001. Предусмотреть печать значений точного решения y=e^x+x.

Преобразуем y΄=p

p΄=3p-2y+2x-3

y(0)=1

p(0)=2.

Нужен массив Х – значений Х от 0 до 2

У – массив приближенных решений

Р – массив значений производной

Размерность –

(a-b)/h+ начальная точка = 2/0,2=10+1=11

Рассмотренный метод Эйлера относится к группе одношаговых методов, в которых для расчета точки (x_i₊₁, y_i₊₁) требуется информация о последней вычислительной точке (x_i, y_i).

Численное решение состоит в построении таблицы приближенных значений y₁, y₂, y₃, …,y_n_-1 точного решения y(x) уравнения y¢=f(x,y), a£x£b при начальном условии y(x₀)=y₀, x₀=a на выбранной последовательности точек x_i=x₀+ih. Функция y зависит от аргумента х

y(x_i+1)=y(x_i)+h f(x_i, y(x_i)), i=0,1,2,…n-1

нет

Точность метода или ошибкой обрыва называют ошибку, которую делают при переходе от предыдущего к последующему Х, если заменяют дифференциальное уравнение конечностным выражением.

Погрешность аппроксимации разностными уравнениями равна величине отброшенного остаточного члена ряда Тейлора O(h^p⁺¹).

Принято считать, если расчетные формулы численного метода согласуются с разложением в ряд Тейлора до членов порядка h^p, то число р называют порядком точности метода.

В методе Эйлера сравнение формулы вычисления с разложением в ряд Тейлора согласуется до первого порядка по h, т.е. метод имеет первый порядок точности с локальной погрешностью O(h²)

Для метода Эйлера погрешность равна h².

10.2. ЧИСЛЕННЫЙ МЕТОД ПОСТРОЕНИЯ ГРАФИКОВ

При решении задач на ЭВМ важное значение имеет наглядность и удобство быстрого восприятия изучаемых явлений. После освоения средств графического режима Турбо Паскаля можно строить графики, а также получать различные геометрические фигуры. Какие бы изображения не выводились на экран, все они строятся из точек, группы которых в свою очередь образуют отрезки и кривые. Вывод точки осуществляется процедурой PutPixel(X, Y, Color), где Х и Y-координаты экрана, где будет расположена точка. Color — ее цвет.

Для построения графика функции необходимо осуществить следующие операции:

1) Табулирование функции;

2) Нахождение максимального и минимального значений функции;

3) Формирование и вывод графика на экран.

Рассмотрим применение графического режима на примере построения графика функции Y(x)= x^з/(2(x+1)(x + 1)) в области изменения х Î [-5,-1)U(-1, 5] с шагом h, а также построения асимптоты, заданной выражением Y(x) = х/2 - 1.

Табулирование функции можно осуществить с помощью следующих операторов:

х := xStart;

h : = (xEnd - xStart) / (n - 1) ;

for i : = 1 to n do begin

y[ i ] :=F(x);

if y[ i ] < - 6 then

y[ i ] := - 6;

x : = x + h;

end;

Здесь введены имена переменных: xStart — начальное значение аргумента, xEnd — конечное значение аргумента, n — число точек в строке. Шаг изменения аргумента X определяется выражением:

h := (xEnd -xStart )/( n - 1);

В организованном цикле табулирования функции вычисляются значения Y(x), используя подпрограмму — функцию с именем F. Индекс каждого значения Х и соответствующее ему значение Y(x), будут помещаться в определенные элементы массива У. В точке Х=-1 заданная функция не определена, поэтому необходимо исключить из построения участок графика в окрестности этой точки. Это достигается программным путем применением операторов

if y[ i ] < - 6 then y[ i ] := - 6;

В данном случае осуществлено ограничение снизу на уровне У=-6, и все значения функции, которые меньше -6, будут исключены из построения графика. В том случае, если в окрестности точки разрыва функция получала бы положительное значение, следовало бы осуществлять ограничение сверху введением операторов

if y[ i ]>a then

y[ i ] :=a;

где а — уровень ограничения.

Для определения масштаба вычерчиваемого графика необходимо найти минимальное и максимальное значения элементов массива Y. Это достигается с помощью операторов

уМах:=у[ 1 ];

yMin :=y[ 1 ];

for i := 1 to n do begin

if y[ i ] > yMax then

yMax := y[ i ];

if y[i] < yMin then

yMin := y[i];

end;

В результате выполнения этого фрагмента программы минимальное значение функции будет храниться в переменной yMin, а максимальное значение — в переменной yMax. Эти значения используются для задания масштаба, чтобы минимальное и максимальное значения функции изображались точками, отстоящими друг от друга не более чем на ширину экрана. Кроме того, они используются при формировании вертикальной и горизонтальной сетки, а также при задании оси абсцисс. Зависимости, по которым определяются эти параметры, приводятся в программе с подробными комментариями.

Для того, чтобы установить графический режим, необходимо использовать стандартную процедуру InitGraph модуля Graph, которая устанавливает один из возможных графических режимов. Формат процедуры следующий:

InitGraph(имя_драйвера, режим, путь_к_драйверу);

В модуле Graph имеется более 70 подпрограмм. Рассмотрим необходимые процедуры для построения графика функции У= f(x) в заданном интервале изменения Х с заданным шагом h.

Для формирования заголовка графика молено использовать следующие процедуры:

SetTextStule(Font, Direct, CharSize); —процедура вывода текста с указанием вида шрифта, наклона и его размера. Вид шрифта (параметр Font) в модуле Graph определяется константами:

DefaultPont = 0 (матричный шрифт);

TriplexPont = 1 (жирный шрифт);

SmallFont = 2 (тонкий шрифт);

SansSerifPont = 3 (прямой шрифт);

GothicPont = 4 (готический шрифт).

Для определения направления вывода текста используются константы: Horizdir = 0 (слева направо) или VertDir = 1 (снизу вверх).

Третий параметр определяет размер шрифта. Если CharSize = 1, то символы имеют обычные размеры (8х8 пикселей), если Char-Size == 2, то символы имеют размеры 16х16 пикселей. Максимальное значение константы равно 10.

Процедура SetTextJustify (код_горизонтали, код_вертикали) — устанавливает параметры для выдачи текста, в зависимости от кода.

Процедура OutTextXY(X, Y, текст) ; — обеспечивает вывод текста с координаты (X, Y).

При формировании оси X, горизонтальной и вертикальной сетки можно использовать следующие процедуры:

SetLineStile(тип_линии, определение_пользователем/ вид_линии); - определяется тип линии: solidin = 0 (сплошная линия), dottein = 1 (пунктирная линия), centerin = 2 (штрих-пунктирная линия), dashedin = 3 (штриховая линия), user-bitin = 4 (определенная пользователем линия); второй параметр имеет смысл только при userbitln=4, а вид линии задается константой nonnwidth = 1 (обычная толщина) или константой thickwidth = 3 (жирная линия);

SetColor (цвет) — определяет цвет символов и линий.

Для установки курсора в указанную координату используется процедура MoveTo, (X, Y), а для вычерчивания линии от текущей линии до указанной координаты — процедура LineTo (X, Y).

При работе с графическими изображениями необходимо использовать систему координат. В зависимости от выбранного графического режима устанавливается разрешающая способность экрана в 320х200, 640х480 или другое число точек (пикселей). Программным путем можно установить максимальное число пикселей в строке с помощью функции GetMaxX, а число строк— с помощью функции GetMaxY. Начало координат имеет значение (0, 0), центр экрана — (GetMaxX div 2, GetMaxY div 2), а правый нижний угол — (GetMaxX, GetMaxY). При выполнении графических операций всегда указывается, что должен делать курсор, однако сам курсор в графическом режиме невидимый.