Алгоритм нахождения производной сложной функции

1. Выделить внешнюю функцию. Поскольку внешняя функция – это последняя операция, которая выполняется при вычислении значения функции, следует выписать последовательность, в которой происходит вычисление значения функции, и обозначить аргумент последней операции буквой U: После введения новой переменной должна получиться функция, имеющаяся в таблице производных.

2. Выписать производную сложной функции как произведение производной внешней функции на производную ее аргумента.

3. Вернуться к исходному аргументу. При необходимости, повторить проделанные операции.

Пример. Найти производную функции:

a)

► Выделим внешнюю функцию : x → x² → x² + 1 → ;

б) у=sin(2x+1)

y'=cos(2x+1)(2x+1)'= 2cos(2x+1) ◄

Частная производная функции 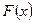в точке по переменной

- производная функции одной переменной при фиксированных значениях других переменных, правила вычисления частной производной и свойства те же;

- она характеризует скорость изменения ФНП в направлении данной координатной оси при фиксированных значениях других координат.

Значение частной производной функции в точке по переменной показывает, на сколько примерно изменится значение функции, если значение аргумента увеличится на единицу, а значения других аргументов не изменятся (это верно, если можно считать приращение аргумента достаточно малым).

ГрадиентФНП в точке – вектор, координаты которого равны частным производным функции в этой точке