Векторы и скаляры
Величины, для задания которых достаточно одного числового значения, называются скалярными. Примерами скаляров могут служить путь, масса, время и т. д.
Величины, для задания которых необходимы числовое значение и направление, называют векторами. Примерами векторов являются, например, перемещение, скорость, ускорение, сила и т. д. Векторы принято обозначать буквами со стрелкой (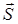 ,
,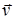 .
.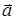 ,
,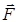 ). При отсутствии стрелки та же буква означает числовое значение или модульсоответствующего вектора. Таким образом,
). При отсутствии стрелки та же буква означает числовое значение или модульсоответствующего вектора. Таким образом, 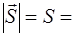 модуль вектора
модуль вектора 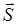 .
.
Модуль вектора – скаляр, причем всегда положительный. Показанная на рис. П. 1а операция сложения векторов символически записывается следующим образом:
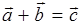 . (П.1)
. (П.1)
|
В результате умножения вектора 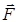 на скаляр а получается новый вектор, модулькоторого в а раз больше вектора
на скаляр а получается новый вектор, модулькоторого в а раз больше вектора  , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора 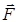 , если скаляр положителен, и противоположно ему, если скаляр отрицателен.
, если скаляр положителен, и противоположно ему, если скаляр отрицателен.
Скалярное произведение двух векторов  и
и  – это скалярная величина, равная произведению модулей векторов
– это скалярная величина, равная произведению модулей векторов  и
и  , умноженному на косинус угла между ними:
, умноженному на косинус угла между ними:
 , (П.2)
, (П.2)
где в формулу введена проекция вектора 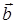 на направление вектора
на направление вектора  (bа= bcosα) (рис. П.1б).
(bа= bcosα) (рис. П.1б).
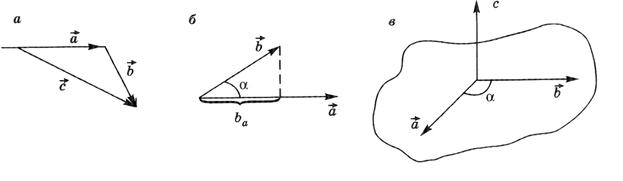
Векторное произведение векторов  и
и  – это вектор
– это вектор  , равный по модулю произведению модулей векторов
, равный по модулю произведению модулей векторов  и
и  на синус угла α между ними (рис. П.1в).
на синус угла α между ними (рис. П.1в).
 , c= absinα, (П.3)
, c= absinα, (П.3)
Вектор 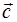 перпендикулярен плоскости, в которой лежат векторы
перпендикулярен плоскости, в которой лежат векторы  и
и  , его направление можно найти, например, по правилу правого буравчика – вращательное движение буравчика должно совпадать с направлением кратчайшего поворота от
, его направление можно найти, например, по правилу правого буравчика – вращательное движение буравчика должно совпадать с направлением кратчайшего поворота от  к
к  , тогда его поступательное движение дает направление
, тогда его поступательное движение дает направление 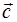 .
.
2. Градиент скалярной величины a. Пусть в пространстве каким-либо образом распределена скалярная величина а– это может быть поле температуры (а= Т), потенциальной энергии (а= U) и т. д. Такое поле можно охарактеризовать градиентом а. Под градиентом скалярной величины понимают вектор, который в каждой точке пространства направлен в сторону наиболее быстрого возрастания аи численно равный приращению величины а на единицу длины этого направления.
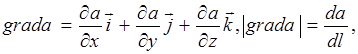 (П.4)
(П.4)
 где
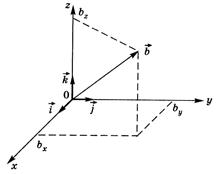
где 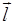 - направление gradaв данной точке пространства; векторы
- направление gradaв данной точке пространства; векторы 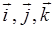 - векторы единичной длины, указывающие направление осей Ох, Оу, Оzв пространстве (рис. П2). Они позволяют представить произвольный вектор
- векторы единичной длины, указывающие направление осей Ох, Оу, Оzв пространстве (рис. П2). Они позволяют представить произвольный вектор  в виде суммы его проекций на оси (рис. П2):
в виде суммы его проекций на оси (рис. П2):
|
 (П.5)
(П.5)
При вычислении производной величины а по координате х в формуле (П.4) считается, что координаты yи zостаются постоянными – такая производная называется частной производной по координате х:
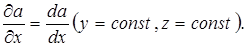
Аналогичные предположения принимаются при расчете частных производных по координатам yи z.
3. Циркуляция и поток вектора .
.
|
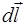 , равный по модулю элементарной длине dlконтура. В каждой точке вектор
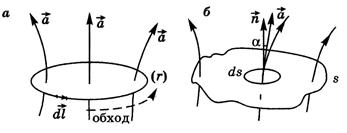
, равный по модулю элементарной длине dlконтура. В каждой точке вектор 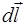 совпадает с касательной к контуру и направлен по обходу контура (рис. П.3а).
совпадает с касательной к контуру и направлен по обходу контура (рис. П.3а).
Тогда циркуляцией вектора по произвольному замкнутому контуру Гназывают интеграл следующего вида:
по произвольному замкнутому контуру Гназывают интеграл следующего вида:
 (П.6)
(П.6)
Можно утверждать, что если для поля вектора  циркуляция вектора
циркуляция вектора  по произвольному замкнутому контуру Гравна нулю, то это поле является потенциальным (например, электростатическое поле вектора
по произвольному замкнутому контуру Гравна нулю, то это поле является потенциальным (например, электростатическое поле вектора 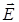 ). Если же циркуляция
). Если же циркуляция  по произвольному замкнутому контуру Готлична от нуля, то поле вектора
по произвольному замкнутому контуру Готлична от нуля, то поле вектора  не является потенциальным, его называют вихревым полем.
не является потенциальным, его называют вихревым полем.
Введем понятие потока Ф вектора  .Возьмем в неоднородном поле вектора
.Возьмем в неоднородном поле вектора  произвольную поверхность S, выделим на ней элементарную площадку dSи введем вектор
произвольную поверхность S, выделим на ней элементарную площадку dSи введем вектор 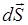 , направленный вдоль вектора нормали
, направленный вдоль вектора нормали 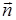 к площадке (рис. П.3б). Модуль
к площадке (рис. П.3б). Модуль 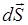 равен площади dSэлементарной площадки.
равен площади dSэлементарной площадки.
Тогда элементарным потоком dФ вектора черезплощадку dSназывают величину
черезплощадку dSназывают величину
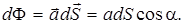
Суммируя потоки dФ через все площадки dSповерхности S, найдем поток вектора  через поверхность S:
через поверхность S:
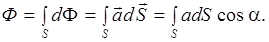 (П.7)
(П.7)
Если учесть, что густота вектора определяет модуль вектора
определяет модуль вектора  в данной точке поля, то тогда поток вектора
в данной точке поля, то тогда поток вектора  численно равен количеству Nлиний
численно равен количеству Nлиний  , пронизывающих поверхность S.
, пронизывающих поверхность S.
4. Дивергенция и ротор вектора  .Для решения практических задач необходимо применять математический аппарат, позволяющий учитывать тип векторных полей не только в большом объеме пространства, но и в малой окрестности какой-либо точки. Для этого вводятся понятия дивергенции (
.Для решения практических задач необходимо применять математический аппарат, позволяющий учитывать тип векторных полей не только в большом объеме пространства, но и в малой окрестности какой-либо точки. Для этого вводятся понятия дивергенции (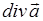 )и ротора (
)и ротора (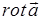 )вектора
)вектора  .
.
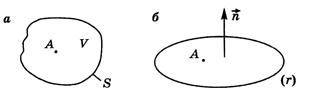
Возьмем объем поля V, ограниченного замкнутой поверхностью S, и будем стягиватьповерхность в малую окрестность точки А(рис. П.4а)
Тогда дивергенцией вектора  называют предел
называют предел
 (П.8)
(П.8)
Дивергенция  характеризует наличие источников первого типа в малой окрестности точки А, например, электрических зарядов (рис. П.5а):
характеризует наличие источников первого типа в малой окрестности точки А, например, электрических зарядов (рис. П.5а):
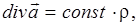 (П.9)
(П.9)
где ρ– плотность заряда.
В математике для 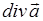 можно записать следующее выражение:
можно записать следующее выражение:
 (П.10)
(П.10)
|
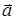 . Возьмем замкнутый контур Г, ограничивающий поверхность S, и будем стягивать контур в малую окрестность точки А (рис. П.4б). Тогда ротором вектора
. Возьмем замкнутый контур Г, ограничивающий поверхность S, и будем стягивать контур в малую окрестность точки А (рис. П.4б). Тогда ротором вектора  называют предел
называют предел
 (П.11)
(П.11)
Ротор (вихрь), например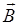 ,характеризует наличие источников полей второго типа в малой окрестности точки А.
,характеризует наличие источников полей второго типа в малой окрестности точки А.
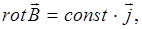 (П.12)
(П.12)
гдеj– плотность электрического тока.
В математике для 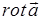 можно записать следующее выражение:
можно записать следующее выражение:
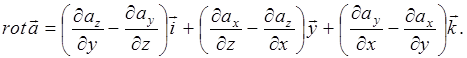 (П.13)
(П.13)