Роль и место PR в маркетинговых коммуникациях
Задание 2
Задание 1
Задания и упражнения
Контрольные вопросы к лекции 16
1. Как зная время ожидания в каждой СМО сети посчитать время ожидания во всей сети?
2. Как моделируется источник заявок в разомкнутой СМО?
3. Какие преобразования сетей называются эквивалентными, а какие толерантными?
4. Какие ограничения и допущения используются при решении задачи синтеза ИС на основе стохастических сетевых моделей?
1. Дан пуассоновский поток с параметром 2 мин-1. Найти вероятность того, что длина интервала между соседними требованиями составляет от 1 до 2 минут.
2. Производится наложение («суперпозиция») двух простейших потоков с интенсивностями 
и 
. Будет ли поток, получившийся в результате наложения, простейшим, и если да, то с какой интенсивностью?
3. Производится случайное прореживание простейшего потока событий с интенсивностью 
; каждое событие, независимо от других, с вероятностью p сохраняется в потоке, а с вероятностью 1-р выбрасывается. Каким будет поток, получающийся в результате прореживания простейшего потока?
4. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 2 машины в минуту. Человек выходит на шоссе, чтобы остановить первую попавшуюся машину, идущую в данном направлении. Найти закон распределения времени Т, в течение которого ему придется ждать машину; определить математическое ожидание и среднее квадратичное отклонение.
5. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 4 машины в минуту. Шоссе имеет развилку в два направления. Вероятность движения машин в первом направлении равна 0,12, а во втором – 0,88. Определить интенсивности движения автомобилей в обоих направлениях.
6. Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону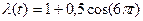 
. Параметр является периодическим, его период равен 1/3. Найти вероятность отсутствия требований на отрезке [1;9].
7. Компьютерный класс связан с каналом Интернет через 10-канальный концентратор. Интенсивности передачи данных по каждому из 10 каналов равны соответственно 540 бит/с, 120 бит/с, 40 бит/с, 170 бит/с, 350 бит/с, 60 бит/с, 742 бит/с, 153 бит/с, 500 бит/с, 100 бит/с. Поток данных подчиняется пуассоновскому закону распределения. Определить интенсивность передачи данных в канале Интернет.
8. Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону 
. Параметр является периодическим, его период равен 1/4. Найти вероятность поступления одного, двух и трех требований.
9. Для простейшего потока с нестационарным параметром, определяемым равенством 
, найти вероятность поступления двух требований на промежутке времени [3;8].
10. По железной дороге мимо наблюдателя движется в одном направлении простейший поток поездов. Известно, что вероятность отсутствия поездов в течение 10 минут равна 0,8. Требуется найти вероятность того, что за 20 мин мимо наблюдателя пройдет не более трех поездов.
11. Производится случайное прореживание простейшего потока событий с интенсивностью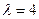 
; каждое событие, независимо от других, с вероятностью p=0,6 сохраняется в потоке, а с вероятностью 1-р выбрасывается. Каким будет поток, получающийся в результате прореживания простейшего потока?
12. Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону 
. Параметр является периодическим, его период равен 1/3. Найти вероятность отсутствия требований на отрезке [1;5].
13. Дан пуассоновский поток с параметром 1 мин-1. Найти вероятность того, что длина интервала между соседними требованиями составляет от 2 до 4 минут.
14. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 8 машин в минуту. Шоссе имеет развилку в три направления. Вероятность движения машин в первом направлении равна 0,12, во втором - 0,68, в третьем - 20. Определить интенсивности движения автомобилей во всех направлениях.
15. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 6 машин в минуту. Человек выходит на шоссе, чтобы остановить первую попавшуюся машину, идущую в данном направлении. Найти закон распределения времени Т, которое ему придется ждать; определить его математическое ожидание и среднее квадратичное отклонение.
16. Для простейшего потока с нестационарным параметром, определяемым равенством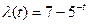 
, найти вероятность поступления двух требований на промежутке времени [1;10].
17. В пункт текущего отделочного ремонта вагонов поступают требования на ремонт. Поток требований можно считать простейшим с интенсивностью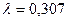 
. Найти вероятность того, что за час не поступит ни одного требования (вагона) на ремонт.
18. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону 
, где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 15 мин.
19. Для простейшего потока с нестационарным параметром, определяемым равенством 
, найти вероятность поступления двух требований на промежутке времени [2;6].
20. В пункт текущего отделочного ремонта вагонов поступает требование на ремонт. Поток требований можно считать простейшим с интенсивностью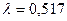 
. Найти вероятность того, что за час поступит одного требование (вагон) на ремонт.
21. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону 
, где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 5 мин.
22. Производится случайное прореживание простейшего потока событий с интенсивностью 
; каждое событие, независимо от других, с вероятностью p=0,75 сохраняется в потоке, а с вероятностью 1-р выбрасывается. Каким будет поток, получающийся в результате прореживания простейшего потока?
23. Производится разбиение случайного простейшего потока событий с интенсивностью 
на три потока. Вероятности попадания событий в тот или иной поток соответственно равны p1=0,2, p2=0,54, p3=0,26. Определить интенсивности каждого получившегося потока в результате разбиения.
24. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону 
, где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 8 мин.
25. В пункт текущего отделочного ремонта вагонов поступают требования на ремонт. Поток требований можно считать простейшим с интенсивностью 
. Найти вероятность того, что за час поступит одно требование (вагон) на ремонт.
26. Производится разбиение случайного простейшего потока событий с интенсивностью 
на 2 потока. Вероятности попадания событий в тот или иной поток соответственно равны p1=0,44, p2=0,56. Определить интенсивности каждого получившегося в результате разбиения потока.
27. Компьютерный класс связан с каналом Интернет через 5-канальный концентратор. Интенсивности передачи данных по каждому из 10 каналов равны соответственно 541 бит/с, 110 бит/с, 44 бит/с, 171 бит/с, 356 бит/с. Поток данных подчинятся пуассоновскому закону распределения. Определить интенсивность передачи данных в канале Интернет.
28. Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону . Параметр является периодическим, его период равен 1/3. Найти вероятность отсутствия требований на отрезке [4;9].
29. На вокзал прибывает пуассоновский поток поездов, в среднем 2 поезда за 5 минут. Найти вероятность того, что за 15 минут прибудут 3 поезда.
30. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону 
, где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 20 мин.
1. В справочной службе вокзала железной дороги стоит телефон с пятью каналами. Приходящий вызов получает отказ тогда, когда все каналы заняты. Пусть среднее время занятости одного канала составляет 1 минуту. Интенсивность поступающих вызовов составляет 0,1 мин-1. Требуется найти вероятность отказа и относительную пропускную способность.
2. На железнодорожной станции находятся три кассы для продажи билетов на поезда дальнего следования. Когда все кассы заняты, пассажиры встают в очередь. Длина очереди не может превышать 50 человек. Среднее время обслуживания в одной кассе составляет 5 минут. Пассажиры прибывают на станцию для покупки билетов в среднем по два человека в минуту. Найти вероятность отказа и общее количество человек (требований), находящихся в системе.
3. Для условия задачи 1 найти вероятность обслуживания вызова, а также вероятность поступления одного вызова.
4. На железнодорожной станции имеется пять путей для обслуживания прибывающих железнодорожных составов. Интенсивность прибытия железнодорожных составов равна 15 составов в час. Среднее время обслуживания одного состава 20 минут. Предполагается, что очередь ожидающих обслуживания поездов может быть неограниченной длины. Найти вероятность занятости всех пяти путей железнодорожной станции и среднее время обслуживания состава.
5. Программист обслуживает вычислительный центр из 50 вычислительных машин (ВМ). В среднем ВМ дает сбой 0,05 час-1. Процесс наладки занимает в среднем 45 минут. Требуется определить абсолютную пропускную способность наладки ВМ программистом.
6. В локомотивном депо обслуживается 100000 железнодорожных вагонов. Каждый вагон в среднем подлежит ремонту один раз в два года. На ремонт вагона затрачивается в среднем 5 дней. Найти вероятность того, что депо занято обслуживанием вагонов.
7. Сервис-центр занимается посреднической деятельностью по продаже железнодорожных билетов и осуществляет часть своей деятельности по 3 телефонным линиям. В среднем в сервис-центр поступает 75 звонков в час. Среднее время обслуживания каждого звонка составляет 2 минуты. Определить вероятность того, что ни один канал не занят, а также вероятность отказа.
8. Преподаватель производит прием экзамена у группы студентов из 23 человек, пришедших в течение одной минуты. Время приема экзамена у одного студента в среднем составляет 20 мин. Студенты, ждущие приема экзамена, находятся в очереди. Определить среднее время ожидания студентом приема экзамена.
9. Для условия задачи 7 определить вероятность занятости одного и двух каналов телефонной линии.
10. В вагоне-ресторане интенсивность обслуживания клиентов в среднем составляет 20 человек в час. Обслуживанием клиентов занимаются два официанта, при этом среднее время обслуживания одного клиента составляет 10 минут. Среднее количество клиентов, покинувших очередь, не дождавшихся обслуживания, составляет 2 человека в час. Определить абсолютную пропускную способность вагона-ресторана.
11. Для условия задачи 7 определить абсолютную пропускную способность сервисного центра.
12. В читальный зал государственной библиотеки, которая имеет 30 посадочных мест, приходят посетители с интенсивностью 20 человек в час. Время пребывания каждого посетителя в среднем составляет 2 часа. Определить вероятность отказа посетителю в читальном зале и среднее число занятых посадочных мест.
13. Абонентский отдел библиотеки обслуживают 3 библиотекаря. Время обслуживания одним библиотекарем читателя в среднем составляет 5 минут. Интенсивность посещения читателями библиотеки составляет 4 человека в минуту. Если в момент прихода читателя все библиотекари заняты, то он встает в очередь. Требуется определить среднее число читателей, ожидающих начала обслуживания и время их пребывания в очереди.
14. Поток заданий в 4-процессорном компьютере является простейшим с интенсивностью 1000 заданий в минуту. Среднее время обработки задания каждым процессором составляет 3 секунды. Если при поступлении задания все процессоры заняты, то задание помещается в очередь (очередь не ограничена). Требуется определить среднюю длину очереди и среднее число занятых процессоров.
15. В компьютерном классе установлен один принтер, скорость печати которого в среднем составляет 2 страницы в минуту. Печать начинается сразу после поступления файла на порт принтера. Среднее время между поступлениями файлов на принтер составляет 1 минуту. Если в момент поступления файла на печать принтер занят, то задания выстраиваются в неограниченную очередь. Требуется определить среднюю длину очереди и общее время пребывания файлов в очереди, если каждый файл в среднем содержит по 5 страниц.
16. На базу данных (БД) сервера железной дороги поступает 10 запросов в секунду. Среднее время обработки каждого запроса составляет 1 секунду. Запрос, поступивший в момент обработки предыдущего запроса, становится в очередь. Определить вероятность наличия очереди и суммарное время, которое проведут запросы до обслуживания.
17. На железнодорожной станции расположена гостиница, в которой имеется 20 мест. Посетитель в случае занятости мест уходит в другую гостиницу. Среднее время снятия гостиницы клиентом составляет 8 часов. Интенсивность потока поступления клиентов составляет 5 человек в час. Определить вероятность отказа и абсолютную пропускную способность данной гостиницы.
18. На телефонной станции железной дороги имеются три линии. Вызов, поступивший, когда все линии заняты, получает отказ. Поток вызовов является пуассоновским с интенсивностью 0,5 вызовов в минуту. Время обслуживания распределено по экспоненциальному закону и в среднем продолжительность разговора составляет 3 минуты. Найти вероятность отказа, относительную и абсолютную пропускные способности и долю свободного времени, приходящегося в среднем на каждую линию.
19. Четырехканальный концентратор имеет буфер емкостью 10 Мб. Пакеты данных поступают на концентратор с интенсивностью 51 пакетов в секунду. Пакеты, поступившие в момент, когда заняты все каналы, выстраиваются в очередь в буфере обмена, если он занят – получают отказ. Средняя скорость одного канала 256 Кб в секунду. Определить абсолютную пропускную способность канала концентратора при среднем размере пакета 2 Кб.
20. Два рабочих обслуживают группу из четырех станков. Остановка рабочего станка происходит в среднем через 30 минут. Время работы и время наладки распределено по экспоненциальному закону. Найти среднюю долю свободного времени для каждого рабочего и среднее время работы станка.
21. Для условия задачи 19 определить вероятность отказа передачи пакета и среднее число свободных каналов концентратора, если средний размер сообщения составляет 5 Кб.
22. Рассмотрим две рядом стоящие телефонные кабины, общая очередь перед которыми не бывает более трех человек («лишние» уходят к другим кабинам). Поток людей, желающих позвонить по телефону, является простейшим и имеет интенсивность 15 человек в час. Время, проводимое людьми в кабине, распределено по экспоненциальному закону и составляет в среднем 3 минуты. Найти среднюю долю времени, когда свободна одна кабина; вероятность того, что человеку придется искать другую кабину.
23. Для условия задачи 20 найти заданные характеристики системы, в которой два рабочих всегда обслуживают станок вместе, причем с двойной интенсивностью.
24. В буфете железнодорожной станции обслуживают клиентов два продавца. Интенсивность обслуживания одним продавцом составляет 0,5 человека в минуту. Посетители приходят в буфет со средним интервалом в 1 минуту. Если в момент прихода клиента все продавцы заняты, клиент встает в очередь, которая не может превышать 5 человек. Посетитель, не попавший в очередь, уходит в другой буфет. Определить вероятность отказа посетителю в обслуживании и среднее время ожидания в очереди.
25. Железнодорожный пропускной таможенный пункт состоит из трех линий досмотра. Время досмотра одного железнодорожного состава на линии досмотра в среднем составляет 4 часа. Интенсивность прибывающих составов составляет 2 состава в час. В случае занятости всех линий досмотра прибывший состав ставится на запасной путь. Определить абсолютную пропускную способность таможенного пункта и среднее время простоя линий досмотра.
26. Железнодорожная сортировочная горка, на которую подается простейший поток составов с интенсивностью 2 состава в час, представляет собой СМО с неограниченной очередью. Время обслуживания (роспуска) состава на горке имеет показательное распределение со средним значением времени 20 мин. Найти среднее число составов в очереди, среднее время пребывания состава в СМО, среднее время пребывания состава в очереди.
27. Автозаправочная станция (АЗС) имеет две колонки. Площадка возле нее допускает одновременное ожидание не более четырех машин. Поток машин, прибывающий на станцию, простейший с интенсивностью 1 машина в минуту. Время обслуживания автомашины распределено по показательному закону со средним значением 2 минуты. Найти для АЗС финальные вероятности состояния для 1, 2,3 и 4-х машин, абсолютную пропускную способность и вероятность отказа в обслуживании.
28. Имеется двухканальная простейшая СМО с отказами. На ее вход поступает поток заявок с интенсивностью 4 заявки в час. Среднее время обслуживания одной заявки 0,8 ч. Каждая обслуженная заявка приносит доход в 4 рубля. Содержание каждого канала обходится 2 руб. в час. Решить: выгодно или не выгодно в экономическом отношении увеличить число каналов СМО до трех, если доход от заявок находится из соотношения D=Ac, где с – доход от обслуженной заявки, А – абсолютная пропускная способность СМО.
29. В зубоврачебном кабинете три кресла, а в коридоре имеются три стула для ожидания приема. Поток клиентов распределен по простейшему закону с интенсивностью 12 клиентов в час. Время обслуживания клиента распределено показательно со средним значением 20 минут. Если все три стула в коридоре заняты, клиенты в очередь не становятся. Определить среднее число клиентов, обслуживаемых кабинетом за час, среднюю долю обслуженных клиентов из числа пришедших и среднее время, которое клиент проведет в коридоре и в кабинете.
30. Билетную кассу с одним окошком представим как СМО с неограниченной очередью. Касса продает билеты в пункты А и В; пассажиров, желающих купить билет в пункт А, приходит в среднем трое за 20 минут, а в пункт В – двое за 20 минут. Поток пассажиров можно считать простейшим. Кассир в среднем обслуживает трех пассажиров за 10 минут. Время обслуживания распределено по показательному закону. Установить, существуют ли финальные вероятности состояний СМО, и если да – вычислить первые три из них. Найти среднее число заявок в СМО, среднее время пребывания заявки в системе и среднее число заявок в очереди.
31. Железнодорожная касса имеет два окошка, в каждом из которых продаются билеты в два пункта: Москву и Петербург. Продажа билетов в оба направления одинакова по интенсивности, которая равна 0,45 пассажиров в минуту. Среднее время обслуживания пассажира (продажи ему билета) 2 минуты. Поступило рационализаторское предложение: для уменьшения очередей (в интересах пассажиров) сделать обе кассы специализированными. В первой продавать билеты только в Петербург, а во второй – только в Москву. Считать все потоки событий простейшими. Требуется проверить разумность этого предложения.
32. Рассматривается простейшая двухканальная СМО с «нетерпеливыми» заявками. Интенсивность потока заявок 3 заявки в час; среднее время обслуживания одной заявки 1 час; средний срок, в течение которого заявка «терпеливо» стоит в очереди, равен 0,5 ч. Подсчитать финальные вероятности состояний, ограничиваясь теми, которые не меньше 0,001. Найти относительную и абсолютную пропускные способности.
33. Ремонтный мастер обслуживает группу из 8-ми кассовых автоматов по продаже билетов в пригородные поезда. Наблюдения показали, что в среднем автомат требует вмешательства мастера раз в 2 ч. Поток требований на ремонт – простейший. Устранение неполадок в автомате занимает в среднем 6 мин, причем время ремонта есть величина случайная, распределенная по показательному закону. Определить коэффициент простоя мастера и среднюю длину очереди автоматов на обслуживание.
34. АТС имеет 6 линий связи. Поток требований на переговоры – простейший с интенсивностью один вызов в минуту. Среднее время переговоров – 3 мин. Закон распределения времени показательный. Определить вероятность отказа и коэффициент загрузки линий связи.
35. На станции метро 5 кассовых аппаратов. Из наблюдений установили, что к этим пяти аппаратам подходят в среднем 60 человек в минуту. Время обслуживания будем считать распределенным по показательному закону, со средним временем обслуживания 4 сек. Найти вероятность того, что все аппараты свободны и среднее число людей, находящихся у аппаратов.
36. В камеру хранения вокзала, состоящую из 5-ти секций, поступает простейший поток требований в среднем 2 требования в минуту. Время обслуживания распределено по показательному закону и составляет в среднем 2 минуты. Время ожидания в очереди составляет в среднем 4 минуты и распределено по показательному закону. Определить среднюю длину очереди, среднее число занятых секций и относительную пропускную способность системы.
37. В железнодорожной поликлинике в кабинете флюорографии проходят прием в среднем 2 человека в минуту. Время приема распределено по показательному закону. Поток посетителей простейший с интенсивностью 5 человек в минуту. Очередь посетителей, ожидающих приема, не ограничена. Определить среднюю длину очереди и абсолютную пропускную способность кабинета флюорографии.
38. Железнодорожная сортировочная горка, на которую подаются простейший поток составов с интенсивностью 2 состава в час, представляет собой СМО с неограниченной очередью. Время обслуживания (роспуска) состава на горке имеет показательное распределение со средним значением времени 15 мин. Найти среднее число составов в очереди, среднее время пребывания состава в очереди, а также абсолютную пропускную способность сортировочной горки.
39. На базу данных (БД) сервера железной дороги поступает 10 запросов в секунду. Среднее время обработки каждого запроса составляет 1 секунду. Запрос, поступивший в момент обработки предыдущего запроса, становится в очередь. Определить вероятность наличия очереди, вероятность отсутствия запроса и коэффициент загрузки сервера.
Чтобы понять роль и место PR в маркетинговых коммуникациях, прежде всего, необходимо понять различия между PR и рекламой внутри коммуникационной стратегии организации.
| Критерий сравнения | Реклама | PR |
| Объект | Товары и услуги | Интересы и идеалы массового сознания |
| Задача | Реализация товаров и услуг | Внедрение и утверждение доминантных моделей общественного мнения, создание благоприятного и предсказуемого климата в общественных отношениях |
| Заказчики, постановщики задач | Производители и продавцы продукции | Менеджмент компаний, правительство, руководство политических партий и общественных организаций. |
| Целевая аудитория | Потребители товаров и услуг | Все члены общества |
Общими у рекламы и PR могут быть каналы распространения информации (коммуникационные каналы) – СМИ, Интернет, прямые контакты представителей организации с целевой аудиторией и т.д.
Целью создания и функционирования любой организации является, как правило, получение прибыли или других благ. Средством достижения поставленной цели является некая яркая жизнеспособная идея (миссия).
Пример: Генри Форд был человеком, которым двигала, в первую очередь, духовная миссия, а во вторую очередь, - деловая миссия. Он хотел сделать автомобиль доступным для масс, а не только для богатых. Вот почему лозунгом его миссии стала «демократизация автомобиля». Когда духовная и деловая миссии обе сильны и согласуются, их совокупная сила создает огромный бизнес.
Таким образом, PR призваны способствовать реализации глобальных идей организации и достижению поставленных ею целей, отвечающих потребностям, как организации, так и общественности.
Теперь можно перейти к пониманию места, занимаемого PR и рекламой внутри бизнес стратегии организации.