ИЗВЛЕЧЕНИЕ КВАДРАТНЫХ КОРНЕЙ ИЗ ЧИСЕЛ И ВОЗВЕДЕНИЕ ИХ В КВАДРАТ.
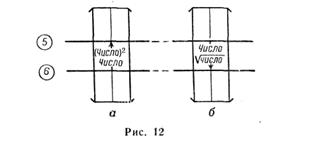
Действия выполняются на шкалах 5 и 6. Деления шкалы 5 нанесены в масштабе, который в два раза меньше масштаба делений шкалы 6, т. е., если соответствующие деления шкалы 6 пропорциональны значениям IgN, то деления шкалы 5 пропорциональны значениям lgN2 = 21gN.
Порядок решения (шкалы 5 и 6):
— установить визирку по шкале 6 на деление, соответствующее основанию степени, или по шкале 5 — на деление, соответствующее степени числа (рис. 12);
— отсчитать по визирке на шкале 5 искомое значение степени (квадрата числа) или по шкале 6 значение основания (корня квадратного из числа).
Примечания: 1. Число знаков квадрата числа равно удвоенному числу знаков основания, если квадрат числа отсчитывается на среднем интервале шкалы 5 (от 10 до 100); или на единицу меньше удвоенного, если отсчитывается на правом или левом интервалах (от 1 до 10 или от 100 до 1000).
2. Число знаков квадратного корня равно числу граней (включая и неполные), если подкоренное число больше или равно 1, или числу чисто нулевых граней, взятому со знаком минус, если подкоренное число меньше единицы; при этом «нуль целых» за грань не считается.
3. Квадратные корни с четным количеством знаков подкоренного выражения извлекаются по среднему интервалу шкалы 5 (10—100), с нечетным количеством знаков— по правому или левому интервалам шкалы 5 (100—1000 или 1—10).
4. Число, возводимое в квадрат, и значение подкоренного выражения можно увеличивать или уменьшать в 10, 100 и т. д. раз и соответственно в 102, 1002 и т. д. раз увеличивать или уменьшать результат.
Примеры:
1) 9,812 = 96,3.
Число знаков результата (1 х 2) = 2.
2) 2,352 = 5,52.
Число знаков результата (1 х 2) —1 = 1.
3) 17,62=309.
Число знаков результата (2 х 2) —1 = 3.
4) 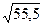 =7,42.
=7,42.
Число граней 1, число знаков результата 1.
5) 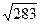 =16,8.
=16,8.
Число граней (неполных) 2, число знаков результата 2.
6) 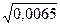 = 0,0807.
= 0,0807.
Число граней (нулевых) 1, число знаков результата —1.
Возведение чисел в квадрат можно производить простым умножением числа на то же число по шкалам 1 и 2 или 14 и 15. Извлечение квадратных корней из чисел возможно также на этих шкалах путем подбора равных значений отрезков шкал. При этом порядок решения будет следующим:
— установить визирку по шкале 15на деление, соответствующее значению числа, из которого извлекается квадратный корень (рис. 13);
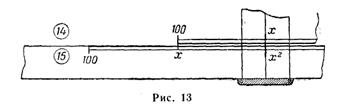
— передвигая движок, добиться такого положения, чтобы на шкале 15против деления 100 или 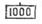 и на шкале 14против риски визирки были равные деления Хпри этом необходимо помнить, что если число знаков подкоренного выражения четное,то движок двигают влево и добиваются равных значений делений против визирки и
и на шкале 14против риски визирки были равные деления Хпри этом необходимо помнить, что если число знаков подкоренного выражения четное,то движок двигают влево и добиваются равных значений делений против визирки и 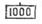 , если же число знаков нечетное,то движок перемещают вправо и добиваются равных значений делений против риски визирки и 100.
, если же число знаков нечетное,то движок перемещают вправо и добиваются равных значений делений против риски визирки и 100.