Отношения на множествах и графы

Каждый ориентированный граф G(X) определяет некоторое от­ношение на множестве X своих вершин. Это отношение может быть записано как x_i G x_j. Оно означает, что в графе есть дуга, идущая от x_i к x_j.

Отношению со свойством рефлексивности (x R х) должна со­ответствовать на графе петля в вершине. Если это отношение со­блюдается во всех вершинах х Î X, то соответствующий граф G(X) должен иметь петлю в каждой своей вершине.

В случае антиреф­лексивного отношения на мно­жестве X, соответствующий граф ни в одной из вершин не имеет петли.

Симметрическому отношению на множестве X соответствует граф с неориентированными ребрами и, наоборот, граф с неориенти­рованными ребрами определяет некоторое симметрическое отношение.

В случае антисимметрического отношения на графе невоз­можно присутствие двух дуг (x_i, x_j), (x_j, x_i) на графе, то есть сущест­вование неориентированного ребра. Кроме того, на этих графах нет петель, то есть соответствующее антисимметрическое отношение антирефлексивно.

Отношение, обладающее свойством тождественности, соот­ветствует графу с антисимметричным отношением на множестве вершин (ориентированному графу) и добавлением петли в каждой вершине. Этот граф не должен иметь контуров.

Рис. 3.18. Свойство транзи­тивности на графе

Граф, соответствующий транзитивному отношению (рис. 3.18), обладает следующи­ми свойствами: для любой пары ориентированных ребер (дуг) графа (x_i, x_j), (x_j, x_k) имеется за­мыкающая дуга (x_i, x_k). Можно сказать, что в графе, который соответствует транзитивному отношению, для каждого пути S(x_i, x_k) имеется дуга (x_i, x_k) (рис.3.19).

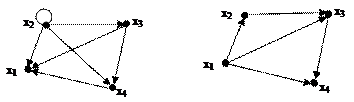
а) б)

Рис. 3.19. Транзитивный (а) и нетранзитивный (б) графы

Отношение, обладающее свойством полноты, опреде­лено на множестве вершин полного ориентированного графа.

Нулевое отношение определено на множестве вершин ноль-графа.

Универсальное отношение определено на множестве вершин полного неориентированного графа с петлями. Дополнительное к R отношение `R определено на множестве вершин дополнительного графа G_d(Х) к G(X).

Графы, соответствующие отношению эквива­лент­ности, пред­ставляют собой совокупность компонент связности (для каждого класса эквивалентности своя компонента) несвязного графа. Каждая компонента несвязного графа должна быть полным неориентиро­ванным графом с петлями (рис. 3.20).

Рис. 3.20. Граф, соответствующий отношению эквивалентности