В жизни любого объекта, как некоторого изделия всегда можно выделить два этапа: производство и эксплуатация данного объекта. Бывает так же этап хранения этого объекта.
Для любого объекта на каждом этапе его жизни задаются определенные технические требования. Желательно, чтобы объект всегда соответствовал этим требованиям. Однако в объекте могут возникнуть неисправности, нарушающие указанное соответствие прибора. Тогда задача состоит в том, чтобы создать на этапе производства или восстановить нарушенную неисправность (которая может появиться на этапах эксплуатации или хранения) в соответствии с заданными техническими требованиями прилагаемыми объекту.
Решение этой задачи невозможно без эпизодического или непрерывного диагноза состояния объекта. Состояние объекта определяется его надежностью. Надежность: это свойство объекта выполняемых заданных функций сохранения, во время значений и установленных эксплуатационных показателей в заданных режимах и условиях использования, технического обслуживания, ремонта и т.д.
Исправное состояние: это состояние, при котором прибор соответствует всем требованиям устнормативной – технической документации.
Неисправное состояние: это состояние, при котором прибор, объект не соответствует хотя бы одному из требований нормативно – технической документации.
Работоспособное состояние: это состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения заданных нормативов в пределах установленных документацией.
Неработоспособное состояние: это состояние, при котором значения хотя бы одного заданного параметра не соответствуют нормативно – технической документации.
Понятие повреждение заключается в нарушении исправного состояния изделия при сохранении его работоспособности. Для любого изделия существуют понятия: дефект, неисправность, отказ, сбой и ошибка.
Дефект: это отклонение от параметров изделия относительно заданных в нормативно – технической документации.
Неисправность: форматированное представление факта проявления дефекта на входах и выходах изделия.
Отказ: дефекты, связанные с необратимыми нарушениями характеристик изделия, приводящим к нарушению его работоспособного состояния.
Сбой: дефект, заключающийся в том, что в результате временного изменения параметров изделия в течение некоторого периода времени оно будет функционировать непрерывно. Причем его работоспособность восстанавливается самонаправленно. Помехи, воздействующие на работоспособность.
Ошибки: (для дискретной техники) называют неправильное значение сигналов на внешних входах изделия, вызванное неисправностями, переходными процессами или помехами, воздействующими на изделие.
Число дефектов, неисправностей, отказов, сбоев, одновременно присутствующих в изделии называют кратностью.
Кратность ошибок определена не только кратностью неисправности, из-за которой она возникла, но и структурной схемой изделия, т.к. в результате имеющихся разветвлений в схеме однократная неисправность может вызвать многократную ошибку в последовательных цепях.
Безотказность: свойство изделия, в котором он непрерывно сохраняет работоспособность в течение некоторого времени.
Ремонтопригодность: свойство изделия, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения его отказов, повреждений и устранения их путем ремонта и технического обслуживания.
Показатели безотказности:
1) Вероятность безотказной работы P(t) – это вероятность того, что в заданном интервале времени t в изделии не возникает отказа.
0£ P(t) £1; P(o) = 1; P(¥) = 0;
Функция P(t) является монотонно убывающей функцией, т.е. в процессе эксплуатации и хранения надежность только убывает. Для определения P(t) используется следующая статическая оценка:
где N – число изделий, поставленных на испытание (эксплуатацию).
N0 – число изделий, отказавших в течении времени t.
2) Вероятность бессбойной работы Рсб(t) – это вероятность того, что в заданном интервале времени t будет отсутствовать сбой в изделии.
Рсб(t) = 1- Q сб(t); где - Q сб(t) функция распределения сбоев в течение времени t.
Для определения стабильности оценки мы имеем формулу:
где N – число изделий поступивших на эксплуатацию.
N0 – число изделий, в которых произошел сбой в течение времени t.
3) Интенсивность отказа l(t) – это условная плотность вероятности возникновения отказа не восстанавливаемого объекта, определенного рассмотренного момента времени, при условии, что до этого момента отказ не возник.
Для определенно l(t) используется следующая статистическая оценка:
где n(Dt) – число отказавших изделий в интервал времени (Dt).
Nср(Dt) – ссреднее число исправных изделий в интервал времени (Dt).
;
4) Средняя наработка до отказа (среднее время безотказной работы) Т – это математическое ожидание наработки до первого отказа определяется так:
Эти показатели рассчитаны на изделие, которое не подлежит восстановлению.
Показатели ремонтопригодности:
1) Вероятность восстановления s(t) – это вероятность того, что отказавшее изделие будет восстановлено в течение времени t.
;
где nв – число изделий время восстановления которых было < (меньше) заданного времени t. Nов – число изделий оставшихся на восстановлении.
2) Интенсивность восстановленного М(t) – условная плотность распространения времени восстановления для момента времени t при условии, что до этого момента восстановление изделия не произошло.
где nв(Dt) – число восстановленных изделий за время Dt. Nв.ср(Dt) – среднее число изделий которые, не были восстановлены в течение времени Dt.
3) Среднее время восстановления Тв – это натуральная величина ожидания восстановления. 
|
Статистическая оценка:
;
4) Коэффициент готовности Кг (t) – это вероятность того, что изделие работоспособно в произвольный момент времени t.
Стационарный режим: t ® ¥.
|
Стационарная оценка: 
;
где tpi i – ый интервал времени исправной работы изделия.
tbi – интервал времени восстановления изделия.
n – число отказов изделия.
Коэффициент оперативной готовности Копер. (t, t) – работоспособна в произвольный момент времени t.
5) Коэффициент оперативной готовности Копер. (t, t) – это вероятность того, что аппаратура будет работоспособна в произвольный момент времени t. и безотказно проработает заданное время r.
Копер.(t, t) = Кг(t) · Р(t)
Для определения Копер. имеется статистическая оценка:
Законы распределения случайных величин, используемые в теории надежности.
Время m/q между соседними отказами для элементов аппарата является непрерывной случайной, величиной, которая характеризует некоторый закон распределения. Наиболее часто используется следующий закон распределения:
Экспонентой распределения Вейбула - называется нормальное распределение Y и другие распределения. Экспоненциальное OCH – показатель надежности при нем могут быть оценены исходя из следующей зависимости
Экспоненциальные показатели - основные показатели надежности при не при них могут оценены исходя из следующей зависимости: P(t) = e-lt; Q(t) = 1 - e-lt; или
l - это параметр экспоненциального распределения.
lt << 1, то Q(t) » lt = 1/Т; P(t) » 1 -lt = 1 –t /T.
Важным свойством экспоненциального распределения является вероятность безотказной работы в интервале t, t +t не зависящем от времени предшествующей работы t, а зависящей от длины интервала t.
Интервалы времени: (0, t); (0; t + t) значит P(t + t) = P(t) · P(t); - вероятность работы системы за время t при условии, что система безотказно проработала за время t.
Для экспоненциального закона ® P(t + t) = e-l(t + t); P(t) = e-lt; P(t) = e-lt.
В интервале времени (t + t) вероятность безотказной работы не зависит от времени работы t, а зависит от t.
Пример.
l = 0,01 (1/час); t = 50 (час).
Значит: Р(50) = е-0б01 · 50 = е-0,05 = 0,0607 Т = 1/l = 100 (час).
Распределение Рема:
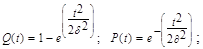
d-параметр распределения Рема.
 |
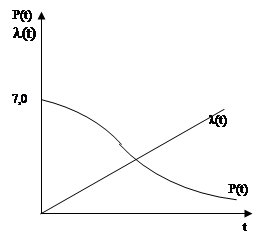Пример: d = 100r, t = 50r.
P(50) =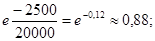 
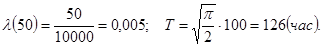
Нормальное распределение:
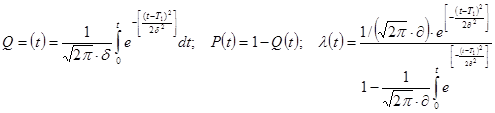
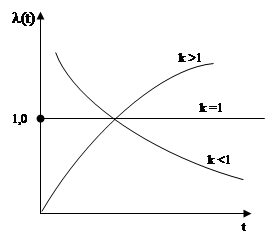
Y – распределение:
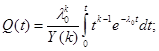
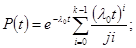
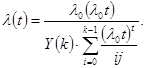
l0, к –параметр. Y-распределение.
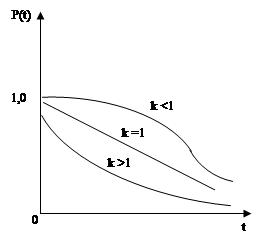При к =1 Y параметр переходит в экспоненциальное распределение.
Распределение Вейбула: 
l1, m – Параметры распределения Вейбула.
 | |||
 | |||
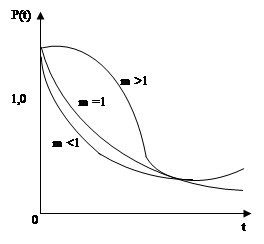При m =1 распределение Вейбула переходит в экспоненту; при m=2 в распределение Релея.
Появление отказов и сбоев можно представить в виде некоторого потока случайного со временем наибольшей переменной в точности получается простейший поток, который характеризуется формулой:
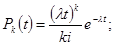
Эта формула позволяет рассчитать вероятность появление отказа в промежутке времени t. Простейший поток характеризует три свойства времени: стационарностью, отсутствием последействия, ординарностью.
Стационарность - указывает, что вероятность появления определенного числа событий за заданный период, времени который не зависит от положений этого периода на оси времени, а зависит только от его действительности.
Отсутствие последействия – характерно тем, что вероятность появления определенного числа событий за заданный период времени независящий от числа и характеризующий события, происходящие до этого времени.
Ординарность - означает не возможность одновременного появления двух и более событий.
Простейший поток получается если:
l(t) = l =cons t; P(t) =e-lt;
С экспоненциальным законом хорошо согласуются законы распределения отказов для сложных систем, состоящих из многих элементов.
Это объясняется тем, что закон распределения интервалов м/д соседними событиями в потоке редких случайных событий составленных из многих неизвестных потоков с любыми характеристиками, которые сходятся к экспоненциальному закону.
|
 |
(0, t1) - первый период повышенных интенсивных отказов. Это связано с выявлением дефектов при изготовлении.
(t1, t2) – второй период, характеризующий постоянные значения интенсивных отказов. Это участок нормальной эксплуатации изделия.
(t2, ¥) Третий период, характеризующий повышенную интенсивность отказов. Здесь начинается процесс старения.
Второй период характеризует эксплуатацию и распределение.
Первый и третий период характеризует распределение Вейбула.
При m < 1 распределение Вейбула можно использовать для оценки надежности изделий при наработке стажа по прошествии времени.
Методы расчета надежности.
Для расчета надежности радиоэлектронной аппаратуры в зависимости от ее надежности (не восстанавливаемость и восстанавливаемость), все зависит от режима обслуживания, от условий хранения, от структуры использования различных методов расчета надежности.