Прочность деталей машин

Лекция 2

Информационные ресурсы

 

1) www.cbr.ru/ – Банк России;

2) www.gks.ru/ – Федеральная служба государственной статистики;

3) www.rcb.ru/ – журнал «Рынок ценных бумаг»;

4) www.naufor.ru/ – Национальная ассоциация участников фондового рынка;

5) www.micex.ru/ – Московская межбанковская валютная биржа;

6) www.raexpert.ru/ – Рейтинговое агентство «Эксперт РА»;

7) www.aup.ru/ – Административно-управленческий портал;

8) www.cfin.ru/ – Финансовая электронная библиотека;

9) www.finansy.ru/ – Финансовая электронная библиотека;

10) www.yourfins.ru/ – Финансовая электронная библиотека;

11) www.finbook.biz/ – Финансовая электронная библиотека;

12) www.finiz.ru/ – Газета «Финансовые известия»;

13) www.mirkin.ru/ – Финансовая электронная библиотека;

14) www.ecsocman.edu.ru/ – Федеральный образовательный портал.

 


[1] Терминология центрального банка РФ (Банка России).

[2] Вопросы сбалансированности бюджетов регулируются Разделом IV Бюджетного кодекса РФ.

[3] Вопросы финансирования дефицита определяются ст. 92-96 Бюджетного кодекса РФ.

[4] Вопросы управления государственным долгом регулируются гл. 14 Бюджетного кодекса РФ.

[5] Следует обратить внимание, что рыночная экономика часто называется «капитализм».

[6] Вопросы займа и кредита регулируются Гл. 42 Частью 2 ГК РФ.

[7] Подробно система государственного кредита рассмотрена в §4.4. пособия.

[8] Способы обеспечения обязательств регулируются Гл. 23 Частью 1 ГК РФ.

[9] Понятие, виды, требования к ценной бумаге рассмотрены в Гл. 7 Части 1 ГК РФ.

[10] Термин «Группа Всемирного банка» охватывает все пять учреждений, термин «Всемирный банк» относится лишь к двум из них – МБРР и МАР.

Основные требования к деталям и узлам машин

 

Как определить качество конструкции детали? Совершенство конструкции детали оценивается по ее надежности и экономичности.

Надежность – свойство детали, узла, машины сохранять во времени свою работоспособность.

Экономичность – характеристика, связанная со стоимостью материала, затратами на производство и эксплуатацию.

Основными критериями работоспособности деталей машин являются:

· Прочность

· Жесткость

· Износостойкость

· Коррозионная стойкость

· Теплостойкость

· Виброустойчивость

Для одних деталей важен один критерий, а для других – иной. Например, для крепежных винтов главным критерием служит прочность, а для ходовых винтов суппортов станков – износостойкость или жесткость, или и то и другое.

В соответствии с перечнем критериев работоспособности необходим ответный перечень инженерных методик расчета деталей машин, т.е. расчет на прочность, расчет жесткости и т.д.

Работоспособность деталей машин обеспечивается:

· Выбором соответствующего материала

· Рациональной конструктивной формой

· Расчетом размеров по главным критериям работоспособности.

Прочность является главным критерием работоспособности большинства деталей машин. Детали могут разрушаться вследствие потери статической прочности или в результате потери сопротивления усталости. Потеря статической прочности происходит тогда, когда значение внешней нагрузки превышает несущую способность конструкции. Потеря сопротивления усталости происходит из-за длительного действия переменных нагрузок, превышающих предел выносливости материала деталей (циклическая прочность). Разделение нагрузок на статические (т.е. постоянные) и циклические (периодически меняющиеся) связано с тем, что материалы различно сопротивляются этим видам нагрузки. Конструктор нового оборудования должен в полной мере учитывать особенности расчета по каждому виду нагрузки.

Напряжения – это мера интенсивности внутренних сил сопротивления материала. Внешние силы, действующие на деталь, вызывают появление в нейвнутренних сил сопротивления. Для их определения в каком-нибудь месте пользуются методом сечений.

2.2. Метод сечений. Рассмотрим тело, находящееся в состоянии равновесия под действием сил 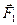, , 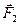и . (силы имеют направление – векторы).

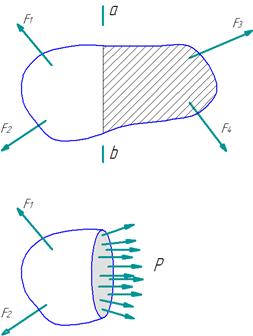Мысленно разрежем тело по сечению «a-b» и отбросим одну из 2-х полученных частей, например, правую. Тогда на оставшуюся левую часть будут действовать внешние силы 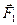, и 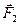. Для того, чтобы часть тела оставалась в равновесии, надо по всему сечению приложить внутренние силы. Будучи внутренними силами для целого тела, они играют роль внешних сил для выделенной части.

Выделим вокруг произвольной точки в сечении малую площадку 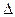А, на эту площадку придется некоторая малая сила 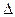Р. Отношение этой силы к площадке дает среднее напряжение на площадке, т.е.

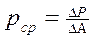; (Па). [ Па = 1 Н/м2 ]

Уменьшая площадку до нуля, т.е. переходя к пределу, постепенно приближаемся к истинному значению напряжения «р» в заданной точке:

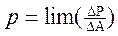при .

Т.к. сила имеет направление, то и напряжение также будет иметь направление. В общем случае напряжение «р» на данной площадке 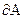будет составлять с этой площадкой некоторый угол. Поэтому вектор «р» полного напряжения в точке сечения можно разложить на два составляющих вектора: σи τ. Вектор σ,направленный перпендикулярно сечению, называется нормальным напряжением. Вектор τ, лежащий в плоскости сечения, называется касательным напряжением. Поскольку векторы σи τ взаимно перпендикулярны, зависимость между числовыми значениями выражается формулой

.

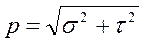Полное напряжение «р» не считается удобной мерой оценки внутренних сил тела, т.к. материалы различным образом сопротивляются нормальным и касательным напряжениям. (Касательные напряжения называют еще напряжениями сдвига)

Растяжение и сжатие (бруса)

Вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – нормальная сила N, называется растяжением или сжатием.

 


Брус растянут, если внешние силы F, приложенные к его концам, действуют вдоль оси бруса и направлены в стороны от бруса. При действии осевых нагрузок F, направленных к брусу, он сжат.

Поперечное сечение бруса обозначим « А ». Наносим риски на расстоянии “ l “.По концам бруса приложены две равные силы F, причем строго по оси бруса. Брус удлиняется в продольном направлении, а поперечные размеры несколько уменьшаются. Удлинение на участке l:

Это приращение длины бруса называется абсолютным (полным) удлинением при растяжении. В случае сжатия оно называется абсолютным укорочением. В относительном виде имеем:

- продольная деформация (при сжатии “ – “ , при растяжении “+”)

- поперечная деформация бруса (“ – “ для растяжения, “+” при сжатии).

Из опытов найдено, что поперечная деформация составляет только некоторую часть от продольной деформации.

- по абсолютной величине, где 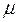- коэффициент Пуассона, зависящий от материала. Так, для стали 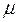= 0,25…0,3.

Закон Гука.В пределах упругих деформаций между нормальным напряжением и продольной деформацией существует прямопропорциональная зависимость:

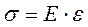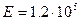, где Е – называется модулем упругости (МПа), выражается в единицах напряжения. Для стали МПа, для меди МПа.

Если в формулу для закона Гука подставить значения

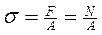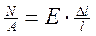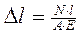; , то получим , или , где

- есть жесткость бруса при растяжении.

2.3. Статические испытания материалов.

Основные механические характеристики

 

Необходимые сведения о механических свойствах конструкционных материалов получают экспериментально. Проводят механические испытания на растяжение, сжатие, срез, кручение и изгиб.

Самыми распространенными являются испытания на растяжение. Для них из испытуемого материала изготавливают стандартные образцы (длина 240 мм, диаметр 10 мм, база l = 100 мм). Образцы испытывают на разрывных машинах, где осевые нагрузки растягивают их и доводят до разрыва. Испытание проводится с контролем силы и удлинения. Поведение материала анализируется из рассмотрения кривой, называемой диаграммой растяжения.

 

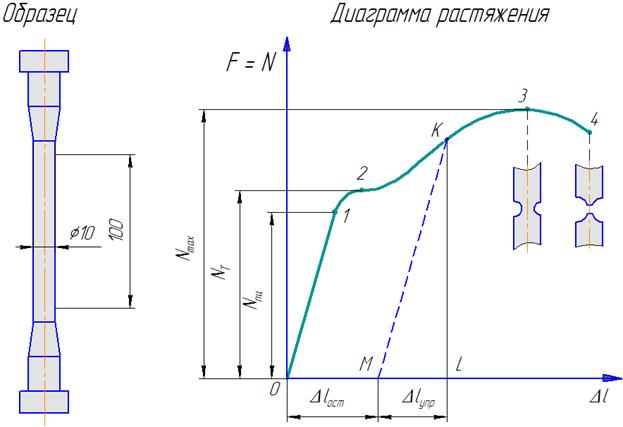
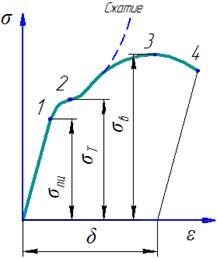
На рисунке примерная диаграмма для образца из низкоуглеродистой стали. По оси абсцисс в определенном масштабе зафиксирован рост удлинения Δl образца. По оси ординат - возникающая в его поперечном сечении нормальная сила N, численно равная осевой нагрузке F, прилагаемой к образцу. Характерные точки на диаграмме отмечены цифрами 1,2,3 и 4.

Вначале испытания (до отметки 1 с ординатой Nпц ) удлинение растет пропорционально силе N, тем самым подтверждается справедливость закона Гука. Далее удлинение Δl возрастает непропорционально силе N. При некотором значении нормальной силы NТ (отметка 2) образец удлиняется без увеличения нагрузки. Это явление называется текучестью металла.

По окончании стадии текучести материал образца снова начинает сопротивляться нагрузке до отметки 3 с ординатой Nmax, после которой наблюдается снижение сопротивляемости образца нагрузке. На образце начинает появляться местное сужение (шейка, точка 3) и в дальнейшем диаграмма фиксирует уже растяжение не всего образца, а только его участка в зоне образовавшейся шейки. Момент окончательного разрушения образца отмечен цифрой 4.

Если после перехода через стадию текучести, например, в момент, отмеченный на диаграмме точкой «К» , образец разгрузить, то процесс разгрузки изобразится отрезком КМ , параллельным отрезку в начале испытания. Как видим, после разгрузки остаточное удлинение Δlост не стало равным удлинению образца, выраженному отрезком OL, а уменьшается на величину упругого удлинения Δlупр.

Теперь, если этот же образец подвергнуть повторному нагружению, то окажется, что линия нагрузки совпадет с линией МК , т.е. часть диаграммы левее этой линии не повторится. Следовательно, после предварительной вытяжки образца за стадию текучести его материал способен воспринимать большие нагрузки без остаточных деформаций. Явление повышения упругих свойств материала в результате предварительной вытяжки выше предела текучести называется наклепом.

Нормальные силы N , возникающие в образце, и его удлинения 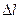зависят от абсолютных размеров образца. Чтобы получить данные по механическим свойствам материала не зависящие от размеров образца, диаграмму перестраивают в координатах (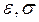). Для этого все абсциссы и ординаты в исходной диаграмме необходимо разделить соответственно на начальную длину l0 и начальную площадь поперечного сечения А0 образца.

Получим:

1. σпц=- предел пропорциональности.

 

2. σТ =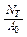- предел текучести.

 

3. σв=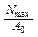- предел прочности (временное сопротивление).

 

4. δ = 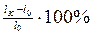- остаточная деформация при разрыве.

При испытании некоторых пластических материалов (медь, алюминий, среднеуглеродистая сталь и др.) на диаграмме растяжения не образуется ясно выраженной стадии текучести. Для таких материалов вводится условный предел текучести, равный напряжению, при котором продольная деформация , т.е. 0,2%. Условный предел текучести обозначается .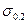

Пластичные свойства материала оцениваются остаточной деформацией при разрыве .

lk и l0 - длины расчетной части образца после и до начала его испытания.

Сжатие. При испытании на сжатие пластические материалы до предела текучести ведут себя так же, как при растяжении. Далее пластическая деформация растет медленнее. Образец постепенно сплющивается (на диаграмме процесс отображен пунктиром).

Хрупкие материалы.

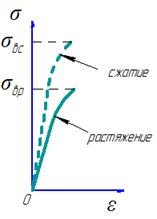При испытании хрупких материалов, например чугунных образцов, установлено, что они способны выдерживать гораздо большие нагрузки при сжатии, чем при растяжении. По этим диаграммам определяют пределы прочности при растяжении и при сжатии.

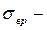предел прочности при растяжении;

предел прочности при сжатии.

Аналогичная диаграмма, но с более высокими значениями ординаты получается для закаленной стали.