МАЛОУГЛОВЫЕ ГРАНИЦЫ

Малоугловые границы образованы системами дислокаций. На рис. 104, б представлена простейшая схема строения малоугловой границы для примитивной кубической решетки. Решетки двух зерен или субзерен упруго сопрягаются, за исключением мест, где оканчиваются неполные атомные плоскости, т. е. где находятся краевые дислокации. Такая граница является стенкой дислокаций одного знака. Линии дислокаций перпендикулярны плоскости чертежа. Два соседних зерна или субзерна симметрично наклонены по отношению к плоскости границы. Поэтому такую малоугловую границу называют симметричной наклонной границей.

Из геометрии симметричной наклонной границы на рис. 104,6 следует, что расстояние между дислокациями в стенке D, вектор Бюргерса их и угол разориентировки зерен 9 связаны следующим соотношением: 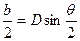. При малых углах sinθ≈θ, тогда

Чем больше угол разориентировки, тем меньше расстояние между дислокациями в стенке. При углах разориентировки более ~10° указанная дислокационная модель неприменима для описания строения границы зерен, так как дислокации располагаются очень близко одна к другой и теряют свою индивидуальность (их ядра сливаются). Поэтому к малоугловым или дислокационным относят межзеренные границы с углом разориентировки не более 10°. Соседние субзерна внутри одного зерна обычно разориентированы на угол не более 1°. Поэтому все субзеренные (блочные) границы малоугловые.

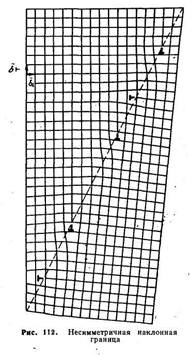
Если малоугловая граница лежит несимметрично, то строение ее усложняется, так как на ней оканчиваются две группы плоскостей, образующие две серии краевых дислокаций (рис. 112).

Малоугловая граница кручения образована рядом винтовых дислокаций (на рис. 113 черные кружки обозначают атомы ниже плоскости границы, а светлые — выше ее).

Граница не может состоять из одного ряда параллельных винтовых дислокаций, так как такой ряд был бы нестабильным. Граница кручения образована сеткой двух взаимно перпендикулярных рядов винтовых дислокаций. Как и в наклонной малоугловой границе, здесь также между участками с несовершенной решеткой (областями ядер дислокаций) имеются участки упругого сопряжения решеток соседних зерен. На рис. 113 такие участки расположены внутри ячеек дислокационной сетки. Рассмотренная дислокационная модель границы кручения, как и наклонной границы, применима только при малых углах разориентировки соседних зерен, так как и здесь (D — расстояние между дислокациями одной серии).

На рис. 104, б, 112 и 113 показаны простейшие дислокационные модели строения границ. В более общем случае малоугловая граница содержит ряды дислокаций разной ориентации и с разным вектором Бюргерса.

Симметричная наклонная граница, являющаяся стенкой краевых дислокаций одного знака с параллельными векторами Бюргерса и параллельными плоскостями скольжения, может легко перемещаться при коллективном скольжении всех дислокаций, входящих в стенку (рис. 114). Такую границу называют скользящей.

В более общем случае малоугловой границы она не может скользить из-за непараллельности плоскостей скольжения составляющих ее дислокаций.

Миграция границы может происходить только диффузионным путем, когда в зависимости от ориентации одни экстраплоскости достраиваются, а другие сокращаются, растворяясь с кромки. Например, на рис. 112 миграция в горизонтальном направлении несимметричной наклонной границы как единого целого должна быть связана с переползанием дислокаций, векторы Бюргерса которых перпендикулярны направлению миграции.

Угол разориентировки зерен или субзерен 0 определяет энергию малоугловой границы:

где Е_о и А — константы (Е_о пропорциональна модулю сдвига и вектору Бюргерса). Согласно этой формуле и многим экспериментальным данным с увеличением θ энергия малоугловой границы непрерывно возрастает.

Малоугловые границы — стенки дислокаций возникают при росте кристаллов из расплава (см. рис. 104), при пластической деформации и при дорекристаллизационном отжиге после холодной деформации. Образование стенок дислокаций, приводящее к подразделению кристалла на субзерна — полигоны (многоугольники), называют полигонизацией.Если, например, до отжига в изогнутом кристалле дислокации были хаотично распределены по плоскостям скольжения (рис. 115, а), то в результате отжига при полигонизации они выстраиваются одна над другой в вертикальные стенки (рис. 115, б)[2]. Как, видно из сопоставления рис. 115, а и б, для выстраивания в стенку необходимо и скольжение, и переползание дислокаций.

Поля упругих напряжений отдельных дислокаций в стенке, накладываясь, в значительной мере взаимно уничтожаются (на рис. 115, 6 под областью разрежения от одной дислокации находится область сгущения от другой дислокации). Этим и обеспечивается стабильность стенки. В результате поле упругих напряжений стенки, внутри которой дислокации отстоят одна от другой на расстоянии D, становится ничтожно малым при удалении по обе стороны от стенки на расстояние больше D. Следовательно, полученная при отжиге — полигонизации стенка дислокаций в отличие от изолированных дислокаций не имеет дальнодействующего поля напряжений. Это относится, естественно, к стенке бесконечно большой протяженности. Стенка конечной протяженности по краям имеет дальнодействующее поле упругих напряжений (из-за его нескомпенсированности).

Малоугловая граница упруго взаимодействует с отдельными дислокациями. На рис. 116 показан один из возможных вариантов такого взаимодействия: дислокации того же знака, что и дислокации в стенке, отталкиваются от стенки в незаштрихованной области и притягиваются к ней в заштрихованных областях. Если дислокация находится в точке Р, то она переползанием может попасть в область притяжения (путь PQ) и затем скольжением пристроиться к стенке, продолжив ее (путь QR). Такое сочетание переползания и скольжения является одним из механизмов полигонизации (см. также рис. 115).

Малоугловая граница притягивает к себе точечные дефекты, в том числе и примесные атомы, вследствие упругого взаимодействия с ними дислокаций, составляющих границу. Это притяжение, как вытекает из сказанного выше, реализуется в зоне, простирающейся всего на несколько межатомных расстояний от границы. Примесные атмосферы тормозят миграцию малоугловых границ, стабилизируя субструктуру.