Динамические испытания на изгиб образцов с надрезом

При динамических испытаниях закон подобия не действует. Поэтому здесь необходима жесткая унификация размеров образцов и условий проведения испытания. Основным образцом по ГОСТ 9454 – 78 служит стержень с квадратным сечением 10×10 мм, длиной 55 мм (рис. 2.68) и надрезом одного из трех видов. U - образный надрез наносится посередине длины. Он имеет ширину и глубину 2 и радиус закругления 1 мм. Допускается использование образцов и шириной B=7,5; 5 и 2 мм. В последнем случае высота H=8 мм.

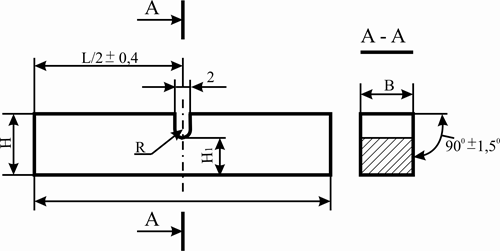
Рисунок 2. 68 - Образец с U–образным надрезом для испытаний на ударный изгиб (ГОСТ 9454–78)

 

Образцы с V – образным концентратором имеют те же габариты и отличаются только геометрией надреза. Третий тип образцов, предусмотренный ГОСТ 9454 – 78, имеет T – образный концентратор (надрез с усталостной трещиной). Длина L этих образцов тоже 55 мм, а высота сечения H=11 мм при B=10; 7,5 или 5 мм. Допускается применение образцов с B=2 мм и H=9 мм, B=H=10 мм и B= H=25 мм. В последнем случае L=140мм.

Образцы с V – образным концентратором являются основными и используются при контроле металлических материалов для ответственных конструкций (летательных аппаратов, транспортных средств и т.д.). Образцы с U – образным надрезом рекомендуется применять при выборе и приемочном контроле металлов и сплавов до установления норм на образцы с V – образным концентратором. Образцы с надрезом и трещиной предназначены для испытания материалов, работающих в особо ответственных конструкциях, где сопротивление развитию трещин имеет первостепенное значение.

При испытании образцов с L=55 мм расстояние между опорами должно быть 40 мм. Изгибающий нож имеет сечение в виде треугольника с углом при вершине 30° и радиусом закругления 2 мм.

Испытания на изгиб проводят на маятниковых копрах с предельной энергией, не превышающей 300 Дж1. Копры должны соответствовать требованиям ГОСТ 10708 – 82.

Схема испытания приведена на рис. 2.69. Образец кладут горизонтально в специальный шаблон, обеспечивающий установку надреза строго в середине пролета между опорами. Удар наносят со стороны, противоположной надрезу, в плоскости, перпендикулярной продольной оси образца.

Маятник копра закрепляется в исходном верхнем положении. По шкале фиксируется угол подъема маятника α. Затем крепящую защелку вынимают, маятник свободно падает под собственной тяжестью, ударяет по образцу, изгибает и разрушает его, поднимаясь относительно вертикальной оси копра на угол β. Этот угол тем меньше, чем большая работа K (при испытании стандартных образцов обозначается KU, KV или KT в зависимости от геометрии надреза) затрачена маятником на деформацию и разрушение образца.

Величина работы деформации и разрушения определяется разностью потенциальных энергий маятника в начальный (после подъема на угол α) и конечный (после взлета на угол β) моменты испытания:

K = P (H – h),

где P – вес маятника; H и h – высоты подъема и взлета маятника (рис. 2.69).

Если длина маятника L, то h=L(1 - cos β), H=L(1 - cos α) и, следовательно,

K = PL(cos β – cos α).

 

Эта формула и служит для расчета работы K по измеренным углам α и β (P и L постоянны для данного копра). Шкала копра может быть проградуирована в единицах работы, если угол подъема маятника α фиксирован.

Зная полную работу деформации и разрушенияK, можно рассчитать основную характеристику, получаемую в результате испытаний – ударную вязкость:

KC = K/F, (2.26)

где F – площадь поперечного сечения образца в месте надреза до испытания.

Стандартная размерность ударной вязкости Дж/см² или кгс∙м/ см^2* .

В зависимости от вида концентратора в образце в обозначение ударной вязкости вводится третий индекс (U, V или T). Например, KCV – ударная вязкость, определенная на образце с V – образным концентратором при комнатной температуре. Допускается обозначение ударной вязкости aU, aV , aT.

Ударные испытания, как и статические, можно проводить при отрицательных и повышенных температурах. Методика этих испытаний также регламентирована ГОСТ 9454 – 78. Испытания проводят с использованием тех же образцов, что и при комнатной.

Для обозначения ударной вязкости при пониженной или повышенной температурах используется цифровой индекс, соответствующий температуре испытания. Например, KCT^-60 – ударная вязкость, определенная на образце с Т – образным концентратором при -60° C. В ГОСТ 9454 – 78 рекомендуется при обозначении ударной вязкости указывать также максимальную энергию удара маятника, Дж, глубину концентратора, мм, в испытанном образце и его ширину, мм. Например, KCU⁺¹⁰⁰ 150/3/7,5 – ударная вязкость, определенная на образце с U – образным концентратором при 100°C на копре с максимальной энергией удара маятника 150 Дж при глубине концентратора 3 мм и ширине образца 7,5 мм. Если используется копер с максимальной энергией удара маятника 300 Дж и образец шириной 10 мм с глубиной концентратора 2 мм, то эти данные в обозначение ударной вязкости не вводятся (пишется просто KCU⁺¹⁰⁰).

В массовых динамических испытаниях на изгиб образцов с надрезом ударная вязкость – единственная выходная характеристика испытания. Диаграмма деформации обычно не записывается, так как это сопряжено со значительными экспериментальными трудностями. Общее время испытания измеряется долями секунды, поэтому для фиксации зависимости нагрузки от деформации требуются малоинерционные чувствительные датчики

и быстродействующий прибор для записи диаграмм. Обычно используют пьезокварцевые и шлейфовые осциллографы.

Ударная вязкость – это сложная, комплексная характеристика, зависящая от совокупности прочностных и пластических свойств материала. Работа, затрачиваемая на пластическую деформацию и разрушение, определяется площадью под диаграммой динамического изгиба. Ее величина, следовательно, будет тем больше, чем выше пластичность и уровень напряжений течения на всем протяжении испытания.

Характеристики пластичности – стрелу изгиба и угол загиба – легко определить, сложив две половины разрушенного образца точно так же, как при испытаниях на статический изгиб.

 

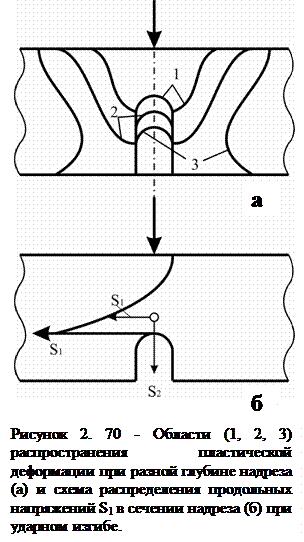
При ударных испытаниях на изгиб образцов с надрезом напряжения и пластическая деформация концентрируются в ограниченной части объема образца вокруг надреза. Именно здесь поглощается практически вся работа удара. На рис. 2.70 а показаны границы области распространения пластической деформации при разной глубине надреза. Видно, что ширина этой области соизмерима с высотой сечения образца и увеличивается по мере уменьшения глубины надреза.

На рис. 2.70 б дана схема распределения продольных нормальных напряжений S₁ в сечении надреза. В районе вершины надреза, помимо S₁, действуют поперечные нормальные напряжения S₂ и S₃ (S₃ не показано на рис. 2.70 б, так как оно перпендикулярно плоскости чертежа). Их появление вызвано торможением поперечной деформации объемами образца, примыкающими с двух сторон к надрезу. Чем глубже и острее надрез и больше ширина сечения, тем больше величина всех трех нормальных напряжений в точке M и меньше работа K.

Повышение ударной вязкости материала часто сопровождается и увеличением деформируемого объема в области надреза.

Возникновение схемы объемного растяжения, концентрация напряжений у надреза, а также рост предела текучести в результате ускорения деформации при мало меняющейся хрупкой прочности (см. схему Иоффе на рис. 2.41) создают наиболее благоприятные условия для хрупкого разрушения.

Количественную величину деформируемого объекта при ударном испытании определить трудно. Поэтому при расчете ударной вязкости полную работу деформации и разрушения относят не к объему, а к площади F поперечного сечения в надрезе, что, строго говоря, не имеет физического смысла. При испытании стандартных образцов величина F постоянна и, следовательно, ударная вязкость прямо пропорциональна полной работе K. Поскольку в разных материалах или при различных температурах испытания пластически деформируются различные объемы, то при одинаковых значениях K получаются разные величины удельной работы (в расчете на единицу объема). Ударная же вязкость в этом случае оказывается одинаковой.

Таким образом, характеристика ударной вязкости KС является условной, и это необходимо учитывать при сопоставлении разных материалов.

Полная работа деформации и разрушения складывается из работ, потраченных на упругую, пластическую деформацию и разрушение. Для того, чтобы количественно определить эти слагаемые K , используют следующий метод. На копре с постепенно увеличивающимся запасом работы маятника (увеличением угла α, рис. 2.69) испытывают несколько образцов и строят зависимость угла загиба от полной работы K (рис. 2.71). Если образцы (при малых углах подъема маятника) не разрушаются, то величину K принимают равной запасу работы маятника

PH = PL(1 - cos α).

Рисунок 2. 71 - Схема определения составляющих работы ударного изгиба (Л. С. Лившиц, А.С. Рахманов)

Угол загиба практически линейно возрастает до определенной величины β_max по мере увеличения поглощенной энергии, а затем остается постоянным. Момент достижения β_max соответствует минимальной работе K_п, при которой уже происходит разрушение. Следовательно, можно считать что после появления трещины у надреза ее дальнейшее распространение не требует дополнительной пластической деформации образца. Тогда работу удара, которая затрачивается только на разрушение (распространение трещины), можно определить как K_разр = K – K_упр - K_пл, где K – полная работа, затраченная маятником (правее точки b на рис. 2.71); K_упр – работа, пошедшая на упругую деформацию (отрезок Oa, отсекаемый восходящей прямой ab на оси абсцисс); K_пл – работа, затраченная на пластическую деформацию.

Температуры, ниже которых K_разр материала близки к нулю, опасны для его практического использования, поскольку возникшая по какой-либо причине трещина может самопроизвольно развиваться, не требуя для своего роста почти никакой подводимой извне энергии.

Чем острее надрез, - тем меньше вклад первых двух слагаемых и больше вклад K_разр в общую работу K. При определении KT и KCT наличие в образцах усталостной трещины делают их величину характеристиками только работы разрушения.

Динамические испытания образцов с надрезом являются самыми жесткими среди стандартных механических испытаний. Поэтому их часто используют для оценки температуры хрупко-вязкого перехода (см.раздел 6.3). Они позволяют выявить эту температуру в тех случаях, когда статические испытания не дают такой возможности (образцы пластичны вплоть до глубоких отрицательных температур). Полезны они и для оценки этой температуры у материалов, которые могут подвергаться ударным нагружениям при эксплуатации. Наконец, ударные испытания часто используют для определения «максимальной» T_хр. Действительно, переход в хрупкое состояние в условиях динамического нагружения происходит при более высоких температурах, чем при статических испытаниях. Поэтому оценка склонности к хрупкому разрушению в наиболее жестких условиях представляет самостоятельный практический интерес.

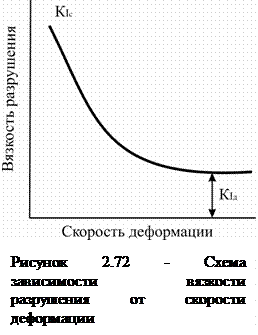
Помимо ударной вязкости по результатам ударных испытаний можно определить динамическую вязкость разрушения K_Iд. Ее величина меньше статической K_Iс, поскольку с увеличением скорости деформации вязкость разрушения снижается (рис. 2.72).

Для экспериментального определения K_Iд можно использовать стандартный образец с трещиной, но при этом необходимо записывать диаграмму изгиба, чтобы определить разрушающую нагрузку P_max, необходимую для расчета:

K_Iд = (P_maxM)/(BH^1/2)Y,

где B и H – ширина и высота сечения образца; Y – коэффициент, зависящий от отношения длины надреза и трещины к высоте сечения (h/H); M – расстояние между опорами маятникового копра.

По результатам ударных испытаний образцов с надрезом и трещиной может быть определено и критическое раскрытие трещины

δ_сд = 0,5(H – h) (π/180)α,

где α – угол изгиба.

Ударная вязкость, особенно КСТ, и характеристики динамической вязкости разрушения, определяя в основном сопротивление материала разрушению, зависят от состава и структуры металла и сплавов во многом аналогично характеристикам трещиностойкости при статическом нагружении (см. раздел 2.5).

Высокая ударная вязкость (более 20 – 80 Дж/см² у разных групп сплавов) характерна для чистых по примесям, высокопластичных однофазных металлов и сплавов или гетерогенных по структуре сплавов с небольшим количеством избыточных фаз или оптимальными их размерами и распределением. Легирование чаще всего снижает ударную вязкость. Очистка от примесей, особенно приводящих к образованию хрупких избыточных фаз, повышает ударную вязкость.

2.5.4. Испытания на изгиб (Статика)

Применение испытаний на изгиб обусловлено широкой распространенностью этой схемы нагружения в реальных условиях эксплуатации и большей ее мягкостью по сравнению с растяжением, что дает возможность оценивать свойства материалов, хрупко разрушающихся при растяжении. Испытания на изгиб удобны для оценки температур перехода из хрупкого состояния в пластичное (например, у хладноломких о.ц.к. металлов и интерметаллидов).

При испытаниях на изгиб применяют две схемы нагружения образца, лежащего на неподвижных опорах: 1) нагрузка прикладывается сосредоточенной силой на середине расстояния между опорами (рис. 2.55, а) и 2) нагрузка прикладывается в двух точках на одинаковом расстоянии от опор (см. рис. 2.55, б). Экспериментально первую схему реализовать гораздо проще, поэтому она нашла наибольшее распространение. Следует учитывать, что вторая схема «чистого изгиба»во многих случаях обеспечивает более надежные результаты, поскольку здесь максимальный изгибающий момент возникает на определенном участке длины образца, а не в одном сечении, как при использовании первой схемы.

Рисунок 2. 55 - Схемы изгиба сосредоточенной силой (а) и двумя симметричными нагрузками (б) с эпюрами изгибающего момента М

В изгибаемом образце создается неоднородное напряженное состояние, зависящее от геометрии образца и способа нагружения. При чистом изгибе узких образцов с прямоугольным сечением напряженное состояние в каждой точке можно считать линейным. В широких образцах (с отношением ширины к высоте сечения более трех) при обеих схемах изгиба (см. рис. 2.55) создается двухосное напряженное состояние из-за затруднения поперечной деформации. Нижняя часть образца оказывается растянутой, верхняя – сжатой. К тому же напряжения, связанные с величиной изгибающего момента, различны по длине и сечению образца. Максимальные напряжения возникают вблизи поверхности. Все это затрудняет оценку средних истинных напряжений и деформаций, строго характеризующих механические свойства при изгибе.

Образцы для испытаний на изгиб не имеют головок. Это еще одно преимущество по сравнению с растяжением, так как изготовление образцов с головками, особенно из хрупких материалов, значительно сложнее. На изгиб испытывают прямоугольные или цилиндрические стержни. Для определения свойств отливок из чугуна используют цилиндрические образцы диаметром 30±1 и длиной 340 или 650 мм (при растяжении между опорами 300 и 600 мм соответственно). Для исследовательских целей испытания на изгиб обычно ведут на цилиндрических образцах с d₀ = 2÷10 мм и расстоянием между опорами l ≥ 10d₀ или плоских образцах с высотой h = 1÷3, шириной b=3÷15 мм и l ≥ 10h. Для оценки характеристик конструкционной прочности рекомендуется применять образцы большого сечения до 30 х 30 мм.

Испытания на изгиб можно проводить на любой универсальной испытательной машине, используемой для испытаний на растяжение. Образец устанавливают на опорную плиту в нижнем захвате и деформируют изгибающим ножом, крепящимся в верхнем захвате машины. Для уменьшения трения опоры, на которых лежит образец, часто делают из роликоподшипников. Образец изгибается при опускании верхнего или подъеме нижнего захвата. При этом на диаграммной ленте может быть записана диаграмма изгиба в координатах нагрузка Р – стрела прогиба f. Для пластичного материала диаграмма изгиба выглядит так, как показано на рис. 2.56. Если материал мало пластичен, то кривая обрывается в точке b. Знание величины нагрузок P_nu , P_упр , P_т , P_b позволяет определять пределы пропорциональности, упругости, текучести и прочности при изгибе. Напряжения на стадии упругой деформации рассчитывают по обычным формулам сопротивления материалов.

Рисунок 2. 56 - Диаграмма изгиба

Условное нормальное напряжение в крайнем растянутом волокне σ = M/W, где M – изгибающий момент, а W – момент сопротивления сечения. В случае нагружения силой (см. рис. 2.55, а)

M = Pl/4.

Для прямоугольного образца

W =bh²/6,

а для цилиндрического

W = πd/32.

Следовательно, рабочей формулой для расчета упругих напряжений при изгибе образцов прямоугольного сечения является

σ = 3Pl/2bh² (2.20)

а для цилиндрических образцов

σ = 8Pl/ πd. (2.21)

По формулам (2.20) и (2.21) часто рассчитывают все прочностные характеристики при изгибе. Но достаточно точные результаты получаются только при определении пределов пропорциональности и упругости.

Из-за неравномерности распределения напряжений по сечению изгибаемого образца определяют два предела текучести – номинальный и реальный. Номинальный предел текучести при изгибе рассчитывают по формулам (2.20) и (2.21), предполагая, что напряжения линейно возрастают по оси образца до его поверхности, где и достигается заданный допуск на удлинение. Реальный предел текучести определяют с учетом действительного распределения напряжений по сечению как истинное напряжение, при котором в поверхностных волокнах возникает остаточная деформация заданной величины.

На практике чаще находят номинальный предел текучести, используемый в инженерных расчетах. Для большинства металлических материалов он на ~20% выше условного предела текучести при одноосном растяжении.

Предел прочности при изгибе σ можно рассчитать по формулам (2.20) и (2.21) только в случае хрупкого разрушения. При значительных пластических деформациях эти формулы, строго говоря, неприменимы.

Графические методы определения прочностных свойств по первичной диаграмме изгиба (см. рис. 2.56) аналогичны применяемым при растяжении. Допуски на величину деформации при определении σ, σи σ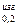 задаются по величине стрелы прогиба, которая связана с относительным удлинением крайнего растянутого волокна в изогнутом образце.

При испытаниях на изгиб, как и в случае сжатия, достаточно пластичные материалы не разрушаются. Образец при этом загибается вплоть до параллельности его частей, расположенных по обе стороны от ножа.

В качестве характеристик пластичности при изгибе используют стрелу прогиба и загиба β, являющийся дополнительным до 180° к углу изгиба α (см. рис. 2.57). Угол β возрастает по мере повышения деформационной способности материала, а угол α уменьшается.

Рисунок 2. 57 - Схема испытаний на трехточечный изгиб

 

 

Лекция разработана «___»________200__г.

 

_______________________Фигуровский Д.К.

 

1 1 Дж ≈ 0,1 кгс·м.

* 1 Дж/см²≈0,1 кгс ∙ м/см²